《2025年名校课堂八年级数学上册华师大版》

13.利用完全平方公式计算$(60\frac{1}{60})^2$的结果为 .

答案： 3602$\frac{1}{3600}$

14.(2024•乐山)已知a-b=3,ab=10,则a²+b²=29.

答案： 29

15.(1)(a+2b-3c)²；解:原式=(a+2b)²-2(a+2b)•3c+(3c)²=a²+4ab+4b²-6ac-12bc+9c².
(2)(a+2b-c)(a-2b-c).解:原式=[(a-c)+2b][(a-c)-2b]=(a-c)²-4b²=a²-2ac+c²-4b².

答案： 解:原式=(a+2b)²-2(a+2b)•3c+(3c)²=a²+4ab+4b²-6ac-12bc+9c².
@@解:原式=[(a-c)+2b][(a-c)-2b]=(a-c)²-4b²=a²-2ac+c²-4b².

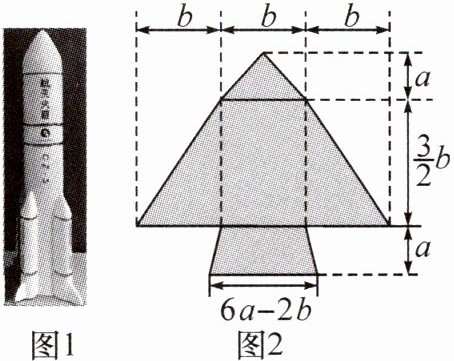
16.新考向 真实情境(2024•南阳卧龙区期中)某校的一个数学兴趣小组参加了学校科技节比赛,制作了如图1所示的航天火箭模型,为了向全校同学宣传自己的科技作品，用KT板制作了如图2所示的宣传版画，它是由一个三角形、两个梯形组成，已知KT板（阴影部分）的尺寸如图2所示.(1)用含a,b的代数式表示图2的KT板模型的总面积(结果需化简)；(2)若a+b=7,ab=$\frac{25}{2}$,求KT板的总面积.解:(1)S总=$\frac{1}{2}$b•a+$\frac{1}{2}$(b+3b)•$\frac{3}{2}$b+$\frac{1}{2}$(b+6a-2b)•a=$\frac{1}{2}$ab+3b²+3a²-$\frac{1}{2}$ab=3b²+3a².(2)∵a²+b²=(a+b)²-2ab=7²-2×$\frac{25}{2}$=49-25=24,∴KT板的总面积为3b²+3a²=3(a²+b²)=3×24=72.

答案： 解:
(1)S总=$\frac{1}{2}$b•a+$\frac{1}{2}$(b+3b)•$\frac{3}{2}$b+$\frac{1}{2}$(b+6a-2b)•a=$\frac{1}{2}$ab+3b²+3a²-$\frac{1}{2}$ab=3b²+3a².
(2)
∵a²+b²=(a+b)²-2ab=7²-2×$\frac{25}{2}$=49-25=24,
∴KT板的总面积为3b²+3a²=3(a²+b²)=3×24=72.

17.新考向 推理能力(教材P44新增习题T6变式)观察下列各式：(2+3)²-2²=7×3；(4+3)²-4²=11×3；(6+3)²-6²=15×3.不难发现规律:比任意一个偶数大3的数与此偶数的平方差能被3整除.
(1)(8+3)²-8²的结果是3的 倍；
(2)设偶数为2n,试说明:比2n大5的数与2n的平方差能被5整除；
(3)比任意一个整数大5的数与此整数的平方差除以10的余数是几？请说明理由.

答案：
(1)19; 
(2)解:
∵偶数为2n,
∴比2n大5的数为2n+5.
∴(2n+5)²-(2n)²=4n²+20n+25-4n²=5(4n+5).
∵4n+5为整数,
∴5(4n+5)能被5整除.
∴比2n大5的数与2n的平方差能被5整除.
(3)余数为5.理由如下:设这个数为n,则比n大5的数为n+5.
∴(n+5)²-(n)²=n²+10n+25-n²=10n+25.
∵10n+25=10(n+2)+5,
∴10n+25除以10的余数是5.
∴比任意一个整数大5的数与此整数的平方差除以10的余数是5.