《2025年名校课堂八年级数学上册华师大版》

11.已知(x + 2)(x - 2) - 2x=1，则2x² - 4x + 3的值为（ ）
A.13
B.8
C.-3
D.5

答案： A

12.(教材P37例3变式)从前，一位庄园主把一块边长为a米(a＞10)的正方形土地租给租户，第二年，他对租户说：“我把这块地的一边增加10米，相邻的另一边减少10米，变成长方形土地继续租给你，租金不变，你也没有吃亏，你看如何?”如果这样，租户的租地面积会（ ）
A.变小
B.变大
C.没有变化
D.无法确定

答案： A

13.【整体思想】如果(2a + 2b + 1)(2a + 2b - 1)=3，那么a + b的值为±1.

答案： ±1

14.计算：(1)(a^m + 1)(a^m - 1)；(2)2023² - 2022×2024.

答案： 解:
(1)原式$=a^{2m} - 1.$
(2)原式=2023² - (2023 - 1)×(2023 + 1)=2023² - 2023² + 1=1.

15.华师二附中校本经典题(2023·南阳宛城区月考)试说明:对于任意整数n，整式(3n + 1)(3n - 1) - (3 - n)(3 + n)的值都能被10整除.
解:原式$=(3n)^2 - 1 - (3^2 - n^2)=9n² - 1 - 9 + n²=10n² - 10=10(n² - 1).$∵n为整数，∴n² - 1为整数，∴10(n² - 1)能被10整除.∴对于任意整数n，原式的值都能被10整除.

答案： 解:原式$=(3n)^2 - 1 - (3^2 - n^2)=9n² - 1 - 9 + n²=10n² - 10=10(n² - 1).$
∵n为整数，
∴n² - 1为整数，
∴10(n² - 1)能被10整除.
∴对于任意整数n，原式的值都能被10整除.

16.石家庄外国语校本经典题(2023·南阳实验学校月考)【探究】如图1，从边长为a的大正方形中剪掉一个边长为b的小正方形，将阴影部分沿虚线剪开，拼成图2的长方形.
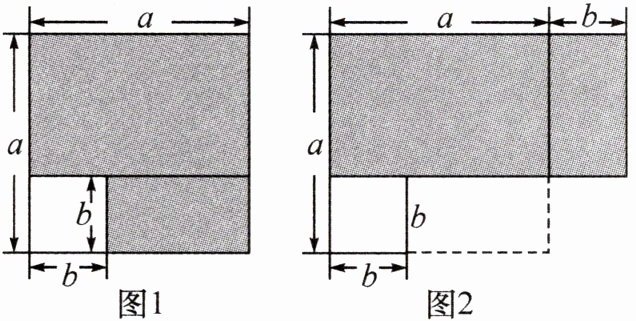
(1)请分别表示出这两个图形中阴影部分的面积：图1： ；图2： ；
(2)比较两个图形中阴影部分的面积，可以得到乘法公式： (用含字母a,b的等式表示)；
【应用】(3)请应用上述公式解答下列各题：①已知2m - n=3，2m + n=4，则4m² - n²的值为 ；②计算:(x - 3)(x + 3)(x² + 9)；
【拓展】(4)计算:(2 + 1)(2² + 1)(2⁴ + 1)(2⁸ + 1)(2¹⁶ + 1)(2³² + 1).

答案： a² - b²; (a + b)(a - b); (a + b)(a - b)=a² - b²; 12;
(3)②解:原式=(x² - 9)(x² + 9)=x⁴ - 81.
(4)解:原式=(2 - 1)(2 + 1)(2² + 1)(2⁴ + 1)(2⁸ + 1)(2¹⁶ + 1)(2³² + 1)=(2² - 1)(2² + 1)(2⁴ + 1)(2⁸ + 1)(2¹⁶ + 1)(2³² + 1)=(2⁴ - 1)(2⁴ + 1)(2⁸ + 1)(2¹⁶ + 1)(2³² + 1)=(2⁸ - 1)(2⁸ + 1)(2¹⁶ + 1)(2³² + 1)=(2¹⁶ - 1)(2¹⁶ + 1)(2³² + 1)=(2³² - 1)(2³² + 1)=2⁶⁴ - 1.