《2025年名校课堂八年级数学上册华师大版》

11. 如图，△ABC是等边三角形，AD为中线，AD＝AE，E在AC上，求∠EDC的度数．
解：∵△ABC是等边三角形，AD为中线，
∴AD⊥BC，∠CAD＝30°．
∵AD＝AE，
∴∠ADE＝∠AED＝$\frac{1}{2}$（180°－∠CAD）＝75°．
∴∠EDC＝∠ADC－∠ADE＝90°－75°＝15°．

答案： 解：
∵△ABC是等边三角形，AD为中线，
∴AD⊥BC，∠CAD＝30°．
∵AD＝AE，
∴∠ADE＝∠AED＝$\frac{1}{2}$（180°－∠CAD）＝75°．
∴∠EDC＝∠ADC－∠ADE＝90°－75°＝15°．

12. 已知△ABC是等腰三角形．若∠A＝70°，则△ABC的顶角度数是 ．
【变式】若等腰三角形的一个角为120°，则另外两个角的度数分别为 ， ．

答案： 70°或40°; 30°; 30°

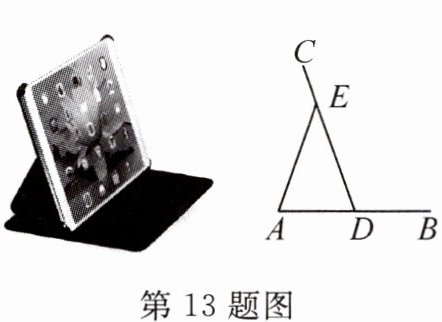
13. 新考向 真实情境 某平板电脑支架及其示意图如图所示，其中AB＝CD，EA＝ED，为了使用的舒适性，可调整∠AEC的大小．若∠AEC增大16°，则∠BDE的度数变化情况是 （D）

A.增大16°
B.减小16°
C.增大8°
D.减小8°

答案： D

14. 如图，点F在正五边形ABCDE的内部，△ABF为等边三角形，则∠AFC＝126°．

答案： 126°

15. 我们规定：等腰三角形的顶角与一个底角度数的比值叫做等腰三角形的“特征值”，记作k．若k＝$\frac{1}{2}$，则该等腰三角形的顶角度数为36°．

答案： 36°

16. 人大附中校本经典题 如图，在△ABC中，点D，E在边BC上，AB＝AC，AD＝AE．求证BD＝CE．

答案：
证明：过点A作AF⊥BC于点F．
∵AB＝AC，AD＝AE，
∴BF＝CF，DF＝EF．
∴BF－DF＝CF－EF，
即BD＝CE．

17. 如图，在等边三角形ABC中，点D，E分别在边BC，AB上，且BD＝AE，AD与CE交于点F．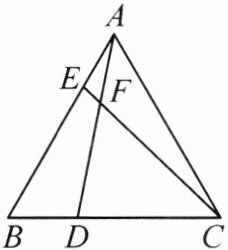
（1）求证：AD＝CE；
（2）求∠DFC的度数．
解：（1）证明：∵△ABC是等边三角形，
∴∠EAC＝∠B＝60°，CA＝AB．
又∵AE＝BD，
∴△AEC≌△BDA（SAS）．
∴AD＝CE．
（2）∵△AEC≌△BDA，
∴∠ACE＝∠BAD．
∴∠DFC＝∠FAC＋∠ACF＝∠FAC＋∠BAD＝∠BAC＝60°．

答案： 解：（1）证明：
∵△ABC是等边三角形，
∴∠EAC＝∠B＝60°，CA＝AB．
又
∵AE＝BD，
∴△AEC≌△BDA（SAS）．
∴AD＝CE．
（2）
∵△AEC≌△BDA，
∴∠ACE＝∠BAD．
∴∠DFC＝∠FAC＋∠ACF＝∠FAC＋∠BAD＝∠BAC＝60°．

18. 如图所示，AOB是一个钢架，且∠AOB＝15°．为了使钢架更加坚固，需在其内部添加一些钢管EF，FG，GH…添加的钢管长度都与OE相等，则最多能添加这样的钢管 （C）

A.2根
B.4根
C.5根
D.无法确定

答案： C