《2025年名校课堂八年级数学上册华师大版》

11. 在△ABC中，∠A，∠B，∠C的对边分别记为a，b，c，则下列说法错误的是（B）

A.若a：b：c=7：24：25，则∠C=90°
B.若∠A：∠B：∠C=3：4：5，则△ABC为直角三角形
C.若a，b，c的长分别为6，8，10，则a，b，c是一组勾股数
D.若∠A－∠B=∠C，则△ABC为直角三角形

答案： B

12. 若△ABC的三边a，b，c满足(a－b)²+|a²+b²－c²|=0，则△ABC是（C）

A.等腰三角形
B.直角三角形
C.等腰直角三角形
D.等腰三角形或直角三角形

答案： C

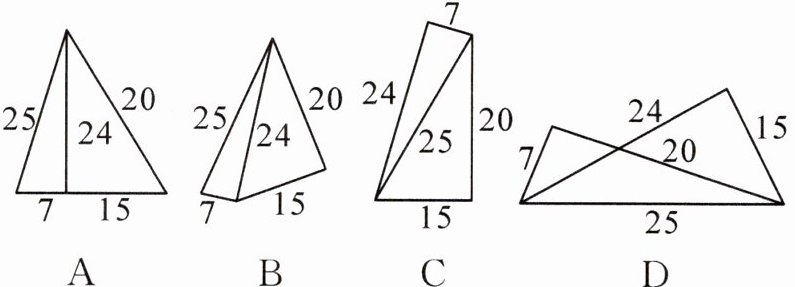
13. 有五根小木棒，其长度分别为7，15，20，24，25，现将它们摆成两个直角三角形，其中正确的是（C）

答案： C

14. （本课时T12变式）若△ABC的三边长a，b，c满足(a－b)(a²+b²－c²)=0，则△ABC为等腰或直角三角形.

答案： 等腰或直角

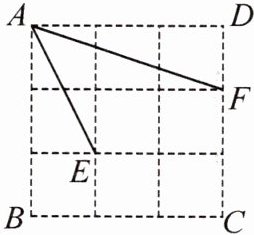
15. （2024·濮阳期末）如图，正方形ABCD是由9个边长为1的小正方形组成的，点E，F均在格点（每个小正方形的顶点都是格点）上，连结AE，AF，则∠EAF的度数是45°.

答案： 45°

16. 小明家有一块四边形地ABCD（如图所示）. 已知其周长为32 m，其中AB=3 m，BC=4 m，CD=13 m，且∠B=90°. 请帮小明计算一下这块地的面积.

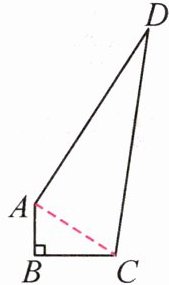
答案： 解：连结AC.
∵AB=3 m，BC=4 m，
∴在Rt△ABC中，根据勾股定理，得AC=√(AB²+BC²)=√(3²+4²)=5(m).
∵四边形ABCD的周长为32 m，
∴AB+BC+CD+DA=32 m.
∴DA=32－AB－BC－CD=32－3－4－13=12(m).在△ACD中，AC²+AD²=5²+12²=169，CD²=13²=169，
∴AC²+AD²=CD².
∴△ACD为直角三角形.
∴S四边形ABCD=S△ABC+S△ACD=1/2×3×4+1/2×12×5=36(m²).答：这块地的面积是36 m².

17. 在一次“探究性学习”课中，老师设计如下数表：

（1）观察表格，根据规律在表中填空；
（2）用含自然数n(n＞1)的代数式表示a，b，c，则a= ，b= ，c= ；
（3）猜想：以a，b，c为边的三角形是否为直角三角形？证明你的结论.

答案： 解：以a，b，c为边的三角形是直角三角形.证明如下：
∵a²+b²=(n²－1)²+(2n)²=n⁴－2n²+1+4n²=n⁴+2n²+1=(n²+1)²=c²，
∴以a，b，c为边的三角形是直角三角形.