第43页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
面积与代数恒等式——教材P53“数学活动”变式1.(2024·南阳期中)如图,将图1中的阴影部分拼成图2,根据两个图形中阴影部分的面积关系,可以验证下列哪个计算公式(
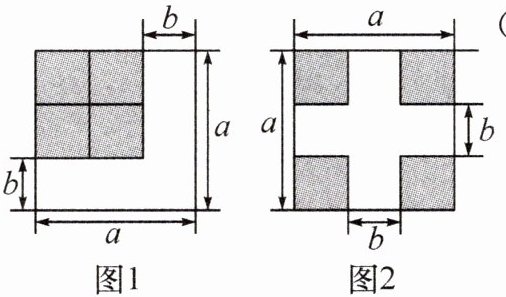
A.a^2-b^2=(a+b)(a-b)
B.(a+b)^2=a^2+2ab+b^2
C.(a-b)^2=a^2-2ab+b^2
D.(a+b)^2=(a-b)^2+4ab
C
)
A.a^2-b^2=(a+b)(a-b)
B.(a+b)^2=a^2+2ab+b^2
C.(a-b)^2=a^2-2ab+b^2
D.(a+b)^2=(a-b)^2+4ab
答案:
C
面积与代数恒等式——教材P53“数学活动”变式2.在学习乘法公式时,课本上通过计算图形面积验证了公式的正确性.下列图形中,不能借助图形面积验证乘法公式$(a+b)(a-b)=a^2-b^2$的是(
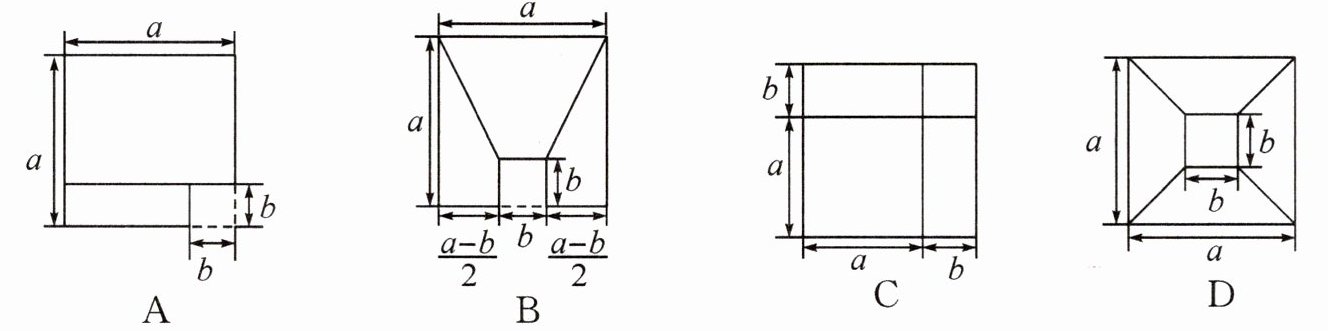
C
)
答案:
C
面积与代数恒等式——教材P53“数学活动”变式3.图形是一种重要的数学语言,它直观形象,能有效地表示一些代数中的数量关系,运用代数思想也能巧妙地解决一些图形问题.请利用数形结合的思想解决以下数学问题.
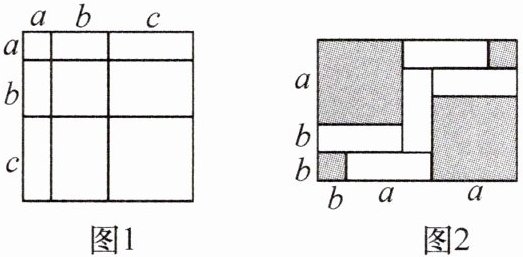
(1)根据图1中大正方形面积的两种不同表示方法,可得出代数恒等式:$(a+b+c)^2=a^2+b^2+c^2+2ab+2bc+2ac;$
(2)如图2,将一张大长方形纸板按图中线段裁剪成9块,其中有2块是边长为a cm的大正方形,2块是边长都为b cm的小正方形,5块是长为a cm,宽为b cm的全等的小长方形,且a>b.
①观察图形,可以发现代数式$2a^2+5ab+2b^2$可以分解因式为 ;
②若阴影部分的面积为$20 cm^2,$大长方形纸板的周长为24 cm,求图2中空白部分的面积.
(1)根据图1中大正方形面积的两种不同表示方法,可得出代数恒等式:$(a+b+c)^2=a^2+b^2+c^2+2ab+2bc+2ac;$
(2)如图2,将一张大长方形纸板按图中线段裁剪成9块,其中有2块是边长为a cm的大正方形,2块是边长都为b cm的小正方形,5块是长为a cm,宽为b cm的全等的小长方形,且a>b.
①观察图形,可以发现代数式$2a^2+5ab+2b^2$可以分解因式为 ;
②若阴影部分的面积为$20 cm^2,$大长方形纸板的周长为24 cm,求图2中空白部分的面积.

答案:
$(a+b+c)^2=a^2+b^2+c^2+2ab+2bc+2ac$; (a+2b)(2a+b)
∵图中阴影部分的面积为$20 cm^2,$
∴$2a^2+2b^2=20,$即$a^2+b^2=10.$
∵大长方形纸板的周长为24 cm,
∴6a+6b=24,即a+b=4.
∴$(a+b)^2=16.$
∴$a^2+2ab+b^2=16.$
∴10+2ab=16.
∴ab=3.
∴空白部分的面积为$5ab=15 cm^2.$
解:
∵图中阴影部分的面积为$20 cm^2,$
∴$2a^2+2b^2=20,$即$a^2+b^2=10.$
∵大长方形纸板的周长为24 cm,
∴6a+6b=24,即a+b=4.
∴$(a+b)^2=16.$
∴$a^2+2ab+b^2=16.$
∴10+2ab=16.
∴ab=3.
∴空白部分的面积为$5ab=15 cm^2.$
查看更多完整答案,请扫码查看


