第48页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
1. 如图,已知线段a,b和∠α,用尺规作△ABC,使BC=a,AC=b,∠ACB=∠α.


答案:
解:如图所示,△ABC即为所求.
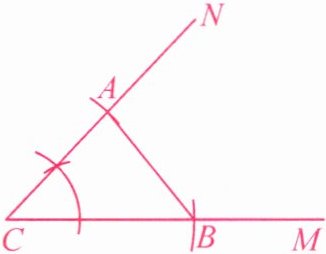
解:如图所示,△ABC即为所求.

2. 下图中的全等三角形是(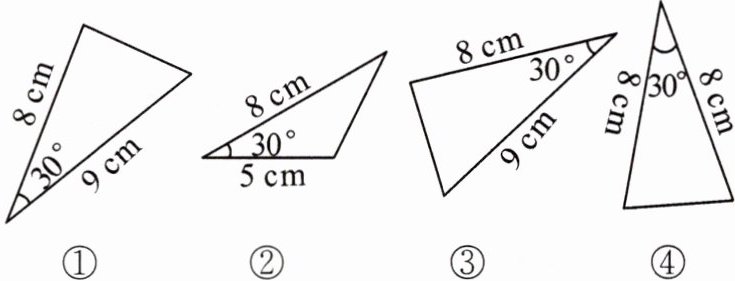
A.①和②
B.②和③
C.②和④
D.①和③
D
)
A.①和②
B.②和③
C.②和④
D.①和③
答案:
D
3. 如图,在△ABC和△DEF中,已知AB=DE,BC=EF,根据“SAS”判定△ABC≌△DEF,还需要的条件是(
A.∠A=∠D
B.∠B=∠E
C.∠C=∠F
D.以上三个均可
B
)
A.∠A=∠D
B.∠B=∠E
C.∠C=∠F
D.以上三个均可
答案:
B
4.(2024·云南)如图,在△ABC和△AED中,AB=AE,∠BAE=∠CAD,AC=AD. 试说明:△ABC≌△AED.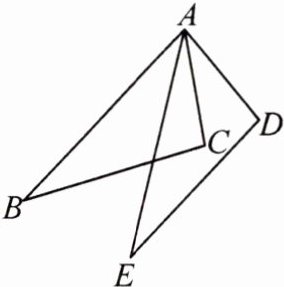

答案:
解:
∵∠BAE=∠CAD,
∴∠BAE+∠CAE=∠CAD+∠CAE,即∠BAC=∠EAD.在△ABC和△AED中,AB=AE,∠BAC=∠EAD,AC=AD,
∴△ABC≌△AED(SAS).
∵∠BAE=∠CAD,
∴∠BAE+∠CAE=∠CAD+∠CAE,即∠BAC=∠EAD.在△ABC和△AED中,AB=AE,∠BAC=∠EAD,AC=AD,
∴△ABC≌△AED(SAS).
5.(2024·安阳期中)如图,已知BF=EC,AB=DE,∠B=∠E,点B,F,C,E在同一条直线上. 求证:∠A=∠D.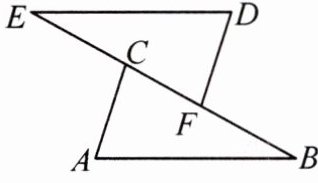

答案:
证明:
∵BF=EC,
∴BF+CF=EC+CF,
即BC=EF.
在△ABC和△DEF中,
AB=DE,∠B=∠E,BC=EF,
∴△ABC≌△DEF(SAS).
∴∠A=∠D.
∵BF=EC,
∴BF+CF=EC+CF,
即BC=EF.
在△ABC和△DEF中,
AB=DE,∠B=∠E,BC=EF,
∴△ABC≌△DEF(SAS).
∴∠A=∠D.
6. 人大附中校本经典题 八(1)班数学兴趣活动小组的同学们利用课余时间制作了圆柱形容器内径测量仪,如图. 制作和使用方法:将两根等长的木棒中心固定在一起,两根木棒可以绕固定点O自由旋转. 测量圆柱形容器内径时,把测量仪的一端放入容器内,再将木棒的两端张开,只要测出露在外面的一端两个木棒之间的距离AD,就知道了容器的内径CB的大小. 请用你学过的数学知识解释测量仪的工作原理(写出已知、求证,并证明).
已知:如图,线段AB,CD相交于点O, ,连结AD,BC.
求证: .
证明:
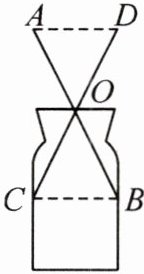
已知:如图,线段AB,CD相交于点O, ,连结AD,BC.
求证: .
证明:
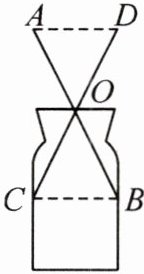
答案:
O为AB和CD的中点(或OA=OB,OD=OC); AD=BC
证明:
∵O为AB和CD的中点,
∴OA=OB,OD=OC.
在△OAD和△OBC中,
OA=OB,∠AOD=∠BOC,OD=OC,
∴△OAD≌△OBC(SAS).
∴AD=BC.
证明:
∵O为AB和CD的中点,
∴OA=OB,OD=OC.
在△OAD和△OBC中,
OA=OB,∠AOD=∠BOC,OD=OC,
∴△OAD≌△OBC(SAS).
∴AD=BC.
查看更多完整答案,请扫码查看


