《2025年名校课堂八年级数学上册华师大版》

11.(2024·广西)如果$a+b=3$，$ab=1$，那么$a^3b+2a^2b^2+ab^3$的值为（ ）
A.0
B.1
C.4
D.9

答案： D

12.运用简便方法计算：
(1)$97^2-3^2=$ ；
(2)$80×3.5^2+160×3.5×1.5+80×1.5^2=$ .

答案： 9400; 2000

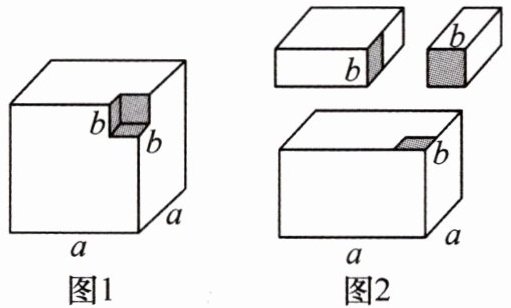
13.是一个棱长为$a$的正方体中挖去一个棱长为$b$的小正方体($a＞b$)，将剩余部分进行切割得到如图2所示的三个长方体.通过计算剩余部分的体积，可对多项式$a^3-b^3$进行因式分解，即$a^3-b^3=$$(a-b)(a^2+ab+b^2)$.

答案： $(a-b)(a^2+ab+b^2)$

14.把下列各式分解因式：
(1)$a^2+4ab+4b^2-1$；
(2)$4x^2-(x^2+1)^2$.

答案：
(1)解:原式$=(a+2b)^2-1=(a+2b+1)(a+2b-1).$
(2)解:原式$=(2x)^2-(x^2+1)^2=(2x+x^2+1)(2x-x^2-1)=(x+1)^2[-(x^2-2x+1)]=-(x+1)^2(x-1)^2.$

15.(2024·南阳官庄一中月考)在分解因式时，小彬和小颖对同一道题产生了分歧，下面是他们的解答过程，请认真阅读并完成相应的任务。

（1）经过讨论，他们发现两人中只有一人的解答正确，则解答正确的同学是 ，这位同学的解答过程中，第1步依据的乘法公式可以用字母表示为 ；而另一位同学的解答是从第 步开始出错的，这位同学解答过程错误的原因是 ；
（2）按照做错同学的思路，写出正确的解答过程.

答案： 小彬; $(a+b)^2=a^2+2ab+b^2$; 1; +2y没有变号
解:原式=(2x+y+x+2y)(2x+y-x-2y)=(3x+3y)(x-y)=3(x+y)(x-y).

16.有一张边长为$a$厘米的正方形桌面，因为实际需要，需将正方形边长增加$b$厘米，木工师傅设计了如图所示的三种方案：

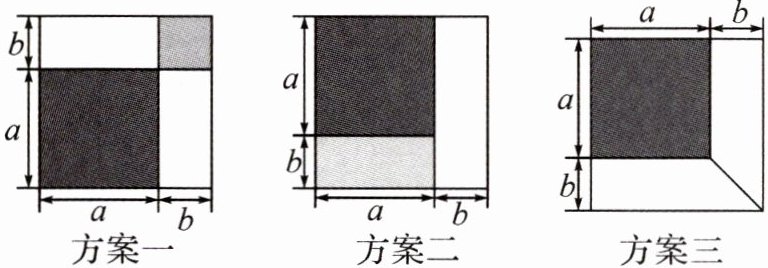
小明发现这三种方案都能验证公式：$a^2+2ab+b^2=(a+b)^2$.
对于方案一，小明是这样验证的：
$a^2+ab+ab+b^2=a^2+2ab+b^2=(a+b)^2$.
请根据方案二、方案三，写出公式的验证过程.

答案： 解:方案二：$a^2+ab+(a+b)b=a^2+ab+ab+b^2=a^2+2ab+b^2=(a+b)^2$.
方案三：$a^2+\frac{[a+(a+b)]b}{2}+\frac{[a+(a+b)]b}{2}=a^2+ab+\frac{1}{2}b^2+ab+\frac{1}{2}b^2=a^2+2ab+b^2=(a+b)^2$.