《2025年名校课堂八年级数学上册华师大版》

1.(2023·洛阳涧西区期中)在学习勾股定理时，甲同学用四个相同的直角三角形(直角边长分别为a,b,斜边长为c)构成如图所示的正方形；乙同学用边长分别为a,b的两个正方形和长为b,宽为a的两个长方形构成如图所示的正方形.甲、乙两位同学给出的构图方案中，可以证明勾股定理的是（ ）

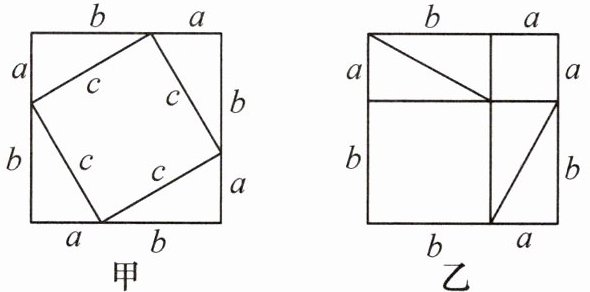
A.甲
B.乙
C.甲、乙都可以
D.甲、乙都不可以

答案： A

2.(2024·南阳方城县期末)如图，已知正方形OABC的边长为1，OA在数轴上，以原点O为圆心，对角线OB的长为半径画弧，交正半轴于一点，则这个点表示的实数是（ ）

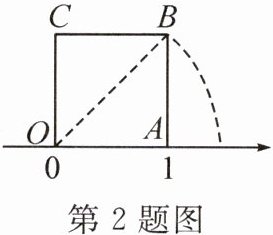
A.1
B.$\sqrt{2}$
C.1.5
D.2

答案： B

3.(2023·鹤壁期末)如图，阴影部分是两个正方形，图中还有一个直角三角形和一个空白的正方形.若阴影部分的面积为25cm²，直角三角形①中较长的直角边长12cm，则直角三角形①的面积是（ ）

A.16cm²
B.25cm²
C.30cm²
D.169cm²

答案： C

4.(2023·南阳方城县期末)在△ABC中，AB=AC，AD是BC上的中线.若AB=10，BC=12，则AD的长为8.

答案： 8

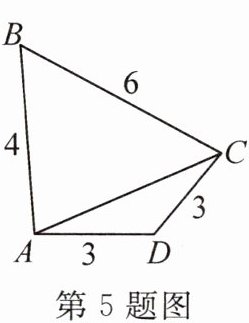
5.四边形ABCD的边长如图所示，对角线AC的长度随四边形形状的改变而变化.当△ABC为等腰三角形时，△ABC的面积为$3\sqrt{7}$.

答案： $3\sqrt{7}$

6.在△ABC中，AB=15，AC=13，边BC上的高AD=12，则△ABC的周长为42或32.

答案： 42或32

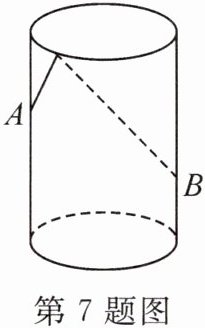
7.(2024·鹤壁外国语月考)如图，圆柱形容器的高为1.2米，底面周长为1米，在容器内壁离容器底部0.3m的点B处有一只蚊子，此时，一只壁虎正好在容器外壁，离容器上沿0.3m且与蚊子相对的点A处，则壁虎捕捉蚊子的最短距离为1.3米.

答案： 1.3

8.【问题情境】某数学兴趣小组想测量学校旗杆的高度.
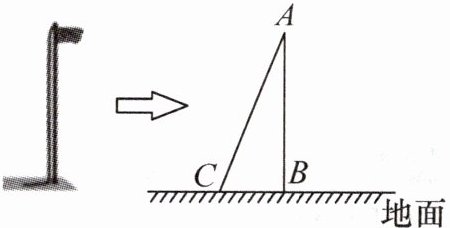
【实践发现】数学兴趣小组实地勘查发现：系在旗杆顶端的绳子垂到了地面，并多出了一段，但这条绳子的长度未知.
【实践探究】设计测量方案：第一步：先测量比旗杆多出的部分绳子的长度，测得多出部分绳子的长度是1米.第二步：把绳子向外拉直，绳子的底端恰好接触地面的点C，再测量绳子底端C与旗杆根部B点之间的距离，测得距离为5米.
【问题解决】设旗杆的高度AB=x米，通过计算即可求得旗杆的高度.(1)依题知BC= 米，AC= 米(用含x的式子表示)；(2)求旗杆的高度.

答案： 5; (x+1) 解：在Rt△ABC中，由勾股定理，得BC²+AB²=AC²，即5²+x²=(x+1)²，解得x=12.答：旗杆的高度为12米.