《2025年名校课堂八年级数学上册华师大版》

12.数学课上，老师讲了单项式乘以多项式，放学回到家，李刚拿出课堂笔记复习，发现一道题“-4xy(3y - 2x - 3) = -12xy²□ + 12xy”，其中□的地方被墨水覆盖了，则□内应填写（ ）
A.+8x²y
B.-8x²y
C.+8xy
D.-8xy²

答案： A

13.(2024·南阳月考)已知A = x² + 3x - a，B = -x，C = x³ + 3x² + 5.若A·B + C的值与x的取值无关，当x = -4时，A的值为（ ）
A.0
B.4
C.-4
D.2

答案： B

14.若x(x² + a) + 3x - 2b = x³ + 5x + 4恒成立，则(a - b)³ =64.

答案： 64

15.某同学在计算一个多项式乘以-3x²时，算成了加上-3x²，得到的答案是x² - $\frac{1}{2}$x + 1，那么正确的计算结果是多少？

答案： 解：设这个多项式为A，则A + (-3x²) = x² - $\frac{1}{2}$x + 1，
∴A = 4x² - $\frac{1}{2}$x + 1.
∴A·(-3x²) = (4x² - $\frac{1}{2}$x + 1)(-3x²) = -12x⁴ + $\frac{3}{2}$x³ - 3x².

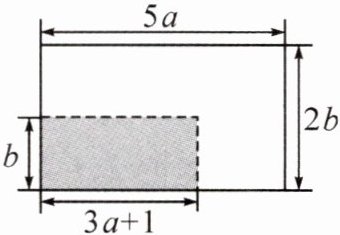
16.某居民小组在进行美丽乡村建设中，规划将一个长为5a m，宽为2b m的长方形场地打造成居民健身场所.如图所示，具体规划如下：在这个场地的一角分割出一块长为(3a + 1)m，宽为b m的长方形场地建篮球场，其余的地方安装各种健身器材，其中用作篮球场的地面铺设塑胶地面，用于安装健身器材的区域铺设水泥地面.
(1)用含a，b的代数式表示篮球场地的面积S₁和安装健身器材区域的面积S₂；
(2)当a = 9，b = 15时，若铺设塑胶地面每平方米需100元，铺设水泥地面每平方米需50元，求建设该居民健身场所所需的铺设地面总费用M(元).

答案： 解：
(1)S₁ = b(3a + 1) = (3ab + b)m²，S₂ = 5a·2b - b(3a + 1) = (7ab - b)m².
(2)当a = 9，b = 15时，M = (3×9×15 + 15)×100 + (7×9×15 - 15)×50 = 88500(元).

17.新考向 阅读理解 阅读下列材料，并解决问题.
已知x²y = 3，求2xy(x⁵y² - 3x³y - 4x)的值.
分析：考虑到满足x²y = 3的x，y的可能值较多，不可以逐一代入求解，故考虑整体思想，将x²y = 3整体代入.
解：2xy(x⁵y² - 3x³y - 4x) = 2x⁶y³ - 6x⁴y² - 8x²y = 2(x²y)³ - 6(x²y)² - 8x²y = 2×3³ - 6×3² - 8×3 = -24.
请用上述方法解决问题：已知ab = 3，求(2a³b² - 3a²b + 4a)·(-2b)的值.

答案： 解：(2a³b² - 3a²b + 4a)·(-2b) = -4a³b³ + 6a²b² - 8ab = -4×(ab)³ + 6(ab)² - 8ab = -4×3³ + 6×3² - 8×3 = -108 + 54 - 24 = -78.