第40页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
1.下列计算正确的是( )
A.a·a^2=a^2
B.(a^3)^2=a^5
C.(-2x)^3=-8x^3
D.(-x)^9÷(-x)^3=-x^6
A.a·a^2=a^2
B.(a^3)^2=a^5
C.(-2x)^3=-8x^3
D.(-x)^9÷(-x)^3=-x^6
答案:
C
2.(2024·南阳卧龙区期中)若m为正整数,则$(\underbrace{m^2+m^2+\cdots+m^2}_{m^2个m})^m=($
A.2m^m
B.m^{2+m}$$
C.m^{m^2}$$
$D.m^{3m}$
D
$)$A.2m^m
B.m^{2+m}$$
C.m^{m^2}$$
$D.m^{3m}$
答案:
D
3.(2024·南阳桐柏县月考)计算$(\frac{5}{7})^{2023}×(\frac{7}{5})^{2024}×(-1)^{2025}$的结果是( )
A.\frac{5}{7}
B.\frac{7}{5}
C.-\frac{5}{7}
D.-\frac{7}{5}
A.\frac{5}{7}
B.\frac{7}{5}
C.-\frac{5}{7}
D.-\frac{7}{5}
答案:
D
4.(1)若2x+3y=4,则4^x·8^y=
(2)若9^b=6,3^a=2,则$3^{3a-2b}=
16
;(2)若9^b=6,3^a=2,则$3^{3a-2b}=
$\frac{4}{3}$
.$
答案:
16; $\frac{4}{3}$
5.(2024·鹤壁期中)如图,从边长为2m+3的正方形纸片中剪出一个边长为m+3的正方形之后,剩余部分可剪拼成一个长方形.若拼成的长方形一边长为m,则拼成的长方形的面积是( )

A.4m^2+12m+9
B.3m+6
C.3m^2+6m
D.2m^2+6m+9

A.4m^2+12m+9
B.3m+6
C.3m^2+6m
D.2m^2+6m+9
答案:
C
6.(2023·南阳卧龙区期中)若3^m÷3^n=27,(9^m)^n=3,则$m^2+n^2=$
10
$.$
答案:
10
7.(2023·南阳宛城区期中)“平方差公式”和“完全平方公式”应用非常广泛,灵活利用公式往往能化繁为简,巧妙解题.观察下列式子,并完成相应任务:
式子1:(x+y-z)(x-y+z)=(A+B)(A-B).
式子2:已知$x^2+y^2=(x+y)^2-P=(x-y)^2+Q.$
任务:
(1)若A=x,则B=
(2)P=Q=
(3)计算:(2a-b+3)(2a-3+b);
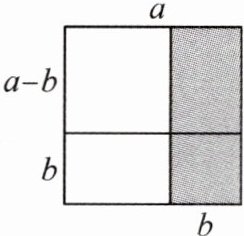
(4)如图,已知在边长为a的正方形中,阴影部分的面积为10,边长为a-b的正方形的周长为12,求$a^2+b^2-ab$的值.
式子1:(x+y-z)(x-y+z)=(A+B)(A-B).
式子2:已知$x^2+y^2=(x+y)^2-P=(x-y)^2+Q.$
任务:
(1)若A=x,则B=
y-z
;(2)P=Q=
2xy
;(3)计算:(2a-b+3)(2a-3+b);
(4)如图,已知在边长为a的正方形中,阴影部分的面积为10,边长为a-b的正方形的周长为12,求$a^2+b^2-ab$的值.
(3)原式=[2a+(3-b)][2a-(3-b)]
$=4a^2-(3-b)^2$
$=4a^2-(9-6b+b^2)$
$=4a^2-9+6b-b^2.$
(4)由题意,得4(a-b)=12,∴a-b=3.
∵阴影部分的面积为10,∴ab=10.
∴原式$=(a-b)^2+2ab-ab$
$=(a-b)^2+ab$
$=3^2+10$
=19.
$=4a^2-(3-b)^2$
$=4a^2-(9-6b+b^2)$
$=4a^2-9+6b-b^2.$
(4)由题意,得4(a-b)=12,∴a-b=3.
∵阴影部分的面积为10,∴ab=10.
∴原式$=(a-b)^2+2ab-ab$
$=(a-b)^2+ab$
$=3^2+10$
=19.

答案:
y-z; 2xy
@@
(3)原式=[2a+(3-b)][2a-(3-b)]$=4a^2-(3-b)^2$$=4a^2-(9-6b+b^2)$$=4a^2-9+6b-b^2.$
(4)由题意,得4(a-b)=12,
∴a-b=3.
∵阴影部分的面积为10,
∴ab=10.
∴原式$=(a-b)^2+2ab-ab$$=(a-b)^2+ab$$=3^2+10$=19.
@@
(3)原式=[2a+(3-b)][2a-(3-b)]$=4a^2-(3-b)^2$$=4a^2-(9-6b+b^2)$$=4a^2-9+6b-b^2.$
(4)由题意,得4(a-b)=12,
∴a-b=3.
∵阴影部分的面积为10,
∴ab=10.
∴原式$=(a-b)^2+2ab-ab$$=(a-b)^2+ab$$=3^2+10$=19.
8.(2024·南阳南召县月考)已知单项式$6x^3y$与$-\frac{3}{2}x^n y^2$的积为$mx^9y^3,$则n的值为(
A.12
B.9
C.6
D.3
C
)A.12
B.9
C.6
D.3
答案:
C
9.(2024·南阳桐柏县月考)现有如图所示的甲、乙、丙三种长方形或正方形纸片各15张,小明要用这些纸片中的若干张拼接(不重叠、无缝隙)一个长、宽分别为5x+4y和3x+y的长方形.则下列判断正确的是(

A.甲种纸片剩余7张
B.丙种纸片剩余10张
C.乙种纸片缺少2张
D.甲种和乙种纸片都不够用
C
)
A.甲种纸片剩余7张
B.丙种纸片剩余10张
C.乙种纸片缺少2张
D.甲种和乙种纸片都不够用
答案:
C
10.(2024·南阳卧龙区期中)下面是两位同学进行整式运算的部分过程,请认真阅读并完成相应的任务.
化简并求值$:[(a+2b)(a-2b)-(a-2b)^2]÷(-2b),$其中$a=-1,b=-\frac{3}{2}.$

任务一:
(1)第①处用到的乘法公式是$(x+y)(x-y)=x^2-y^2;$(用含x,y的式子表示)
(2)第②处错误的原因是
任务二:
(3)小宛运用了因式分解的方法,简便了运算,但其过程不完整,请你补全小宛的过程.
化简并求值$:[(a+2b)(a-2b)-(a-2b)^2]÷(-2b),$其中$a=-1,b=-\frac{3}{2}.$

任务一:
(1)第①处用到的乘法公式是$(x+y)(x-y)=x^2-y^2;$(用含x,y的式子表示)
(2)第②处错误的原因是
完全平方公式运用错误
;任务二:
(3)小宛运用了因式分解的方法,简便了运算,但其过程不完整,请你补全小宛的过程.
解:原式=(a-2b)[(a+2b)-(a-2b)]÷(-2b)
=(a-2b)×4b÷(-2b)
=-2(a-2b)
=-2a+4b.
当$a=-1,b=-\frac{3}{2}$时,
原式$=-2×(-1)+4×(-\frac{3}{2})=2-6=-4.$
=(a-2b)×4b÷(-2b)
=-2(a-2b)
=-2a+4b.
当$a=-1,b=-\frac{3}{2}$时,
原式$=-2×(-1)+4×(-\frac{3}{2})=2-6=-4.$
答案:
$(x+y)(x-y)=x^2-y^2$; 完全平方公式运用错误
@@解:原式=(a-2b)[(a+2b)-(a-2b)]÷(-2b)=(a-2b)×4b÷(-2b)=-2(a-2b)=-2a+4b.当$a=-1,b=-\frac{3}{2}$时,原式$=-2×(-1)+4×(-\frac{3}{2})=2-6=-4.$
@@解:原式=(a-2b)[(a+2b)-(a-2b)]÷(-2b)=(a-2b)×4b÷(-2b)=-2(a-2b)=-2a+4b.当$a=-1,b=-\frac{3}{2}$时,原式$=-2×(-1)+4×(-\frac{3}{2})=2-6=-4.$
查看更多完整答案,请扫码查看


