《2025年名校课堂八年级数学上册华师大版》

易错点 因直角边不确定导致漏解
9. 在Rt△ABC中，AB=8，BC=15，则AC的长是（C）
A.17
B.$\sqrt{161}$或13
C.17或$\sqrt{161}$
D.13或17

答案： C

中档题
10. 在Rt△ABC中，若∠C=90°，AC=3，BC=4，则点C到直线AB的距离为（D）
A.3
B.4
C.5
D.2.4

答案： D

11. （2023·天津）如图，在△ABC中，分别以点A和点C为圆心，大于$\frac{1}{2}$AC的长为半径作弧（弧所在圆的半径都相等），两弧相交于M，N两点，直线MN分别与边BC，AC相交于点D，E，连结AD. 若BD=DC，AE=4，AD=5，则AB的长为（D）

A.9
B.8
C.7
D.6

答案： D

12. 如图，若∠BAD=∠DBC=90°，AB=3，AD=4，BC=12，则CD=13.

答案： 13

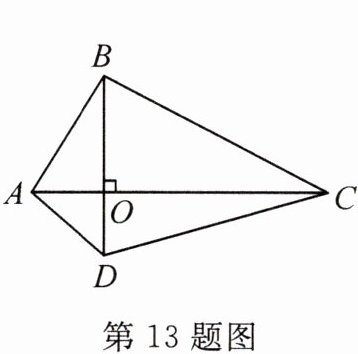
13. （2024·郑州巩义市期末）对角线互相垂直的四边形叫做“垂美”四边形. 现有如图所示的“垂美”四边形ABCD，对角线AC，BD相交于点O. 若AD=2，BC=4，则AB² + CD²=20.

答案： 20

14. （教材P132习题T3变式）如图，∠ACB=90°，AB=4cm，以Rt△ABC的三边为直角边分别向外作等腰直角三角形，则图中阴影部分的面积为16cm².

答案： 16

15. 如图所示，∠B=∠OAF=90°，BO=3cm，AB=4cm，AF=12cm，求图中半圆（阴影部分）的面积.

答案： 解：在Rt△ABO中，BO=3cm，AB=4cm，由勾股定理，得AO=$\sqrt{BO^2 + AB^2}$=5cm.
在Rt△AFO中，AF=12cm，AO=5cm，由勾股定理，得FO=$\sqrt{AO^2 + AF^2}$=13cm.
∴S半圆=$\frac{1}{2}\pi×(\frac{FO}{2})^2=\frac{1}{2}\pi×\frac{169}{4}=\frac{169\pi}{8}$(cm²)

综合题
16. “赵爽弦图”巧妙地利用面积关系证明了勾股定理，是我国古代数学的骄傲. 如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形. 设“赵爽弦图”中直角三角形的较长直角边长为a，较短直角边长为b，若$(a+b)^2=24$，大正方形的面积为14，求小正方形的面积.

答案： 解：设大正方形的边长为c.
则$a^2 + b^2 = c^2 = 14$.
∵$(a+b)^2=24$，
∴$a^2 + 2ab + b^2=24$.
∴ab=5.
∴S小正方形=14 - $\frac{ab}{2}×4$=14 - 2×5=14 - 10=4.