第80页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
探索三角形边、角的关系——教材P97“信息技术应用”变式
阅读下列材料,并完成相应任务.
实验探究:三角形中边与角之间的关系.
问题提出:学习了等腰三角形,我们知道:在一个三角形中,等边所对的角相等;反过来,等角所对的边也相等.那么,不相等的边(或角)所对的角(或边)之间有怎样的大小关系呢?
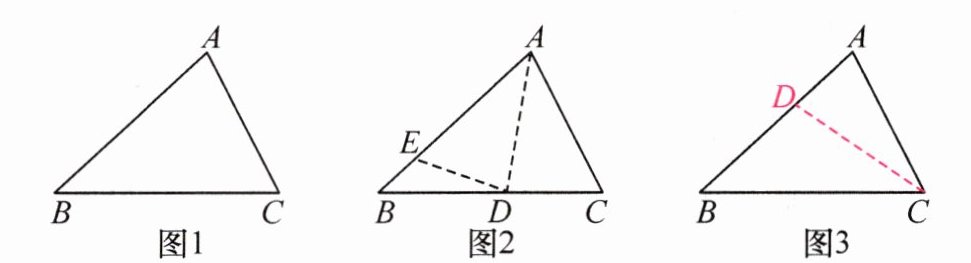
问题具体化:如图1,在△ABC中,AB>AC,则∠C与∠B有怎样的大小关系?
思路分析:解决不等边关系问题时,往往采用在长边上截取短边,使条件和问题转化或聚焦,并构造全等三角形解决问题.
问题解决:如图2,在长边AB上截取AE=AC,作∠BAC的平分线,交BC于点D,连结DE.求证:∠C>∠B.
证明:∵AD平分∠BAC,∴∠EAD=∠CAD.
又∵AD=AD,AE=AC,
∴△AED≌△ACD.(依据1: )_______
∴∠AED=∠C.
∵∠AED=∠B+∠BDE,(依据2: )_______
∴∠AED>∠B.∴∠C>∠B.
得出结论:在一个三角形中,如果两条边不相等,那么它们所对的角也不相等,其中大边 ._______
类比探究:在一个三角形中,如果两个角不相等,那么它们所对的边也不相等,其中大角所对的边较大.
已知:如图3,在△ABC中,∠ACB>∠ABC.求证:AB>AC.
证明:……
任务:
(1)写出“问题解决”中的“依据1”“依据2”:
依据1: ;
依据2: ;
(2)将材料中“得出结论”补充完整: ;
(3)完成“类比探究”部分中的证明过程.
阅读下列材料,并完成相应任务.
实验探究:三角形中边与角之间的关系.
问题提出:学习了等腰三角形,我们知道:在一个三角形中,等边所对的角相等;反过来,等角所对的边也相等.那么,不相等的边(或角)所对的角(或边)之间有怎样的大小关系呢?
问题具体化:如图1,在△ABC中,AB>AC,则∠C与∠B有怎样的大小关系?
思路分析:解决不等边关系问题时,往往采用在长边上截取短边,使条件和问题转化或聚焦,并构造全等三角形解决问题.
问题解决:如图2,在长边AB上截取AE=AC,作∠BAC的平分线,交BC于点D,连结DE.求证:∠C>∠B.
证明:∵AD平分∠BAC,∴∠EAD=∠CAD.
又∵AD=AD,AE=AC,
∴△AED≌△ACD.(依据1: )_______
∴∠AED=∠C.
∵∠AED=∠B+∠BDE,(依据2: )_______
∴∠AED>∠B.∴∠C>∠B.
得出结论:在一个三角形中,如果两条边不相等,那么它们所对的角也不相等,其中大边 ._______
类比探究:在一个三角形中,如果两个角不相等,那么它们所对的边也不相等,其中大角所对的边较大.
已知:如图3,在△ABC中,∠ACB>∠ABC.求证:AB>AC.
证明:……

任务:
(1)写出“问题解决”中的“依据1”“依据2”:
依据1: ;
依据2: ;
(2)将材料中“得出结论”补充完整: ;
(3)完成“类比探究”部分中的证明过程.
答案:
(1)SAS; (2)三角形的一个外角等于与它不相邻的两个内角的和; 所对的角较大;
∴DB=DC.
∴DB+AD>AC,
(3)证明:在∠ACB的内部作∠BCD=∠B,交AB于点D.
∴DB=DC.
在△ADC中,有DC+AD>AC,
∴DB+AD>AC,
即AB>AC.
查看更多完整答案,请扫码查看


