《2025年名校课堂八年级数学上册华师大版》

9.如图,网格中每个小正方形的边长均为1,则△ABC的三边a,b,c的大小关系是（ ）


A.a＜c＜b
B.a＜b＜c
C.c＜a＜b
D.c＜b＜a

答案： C

10.某数学兴趣小组开展了笔记本电脑的张角大小的实践探究活动.如图,当张角为∠BAF时,顶部边缘B处离桌面的高度BC为7cm,此时底部边缘A处与C处间的距离AC为24cm.小组成员调整张角的大小继续探究,最后发现当张角为∠DAF时(D是B的对应点),顶部边缘D处到桌面的距离DE为20cm,则底部边缘A处与E之间的距离AE为（ ）

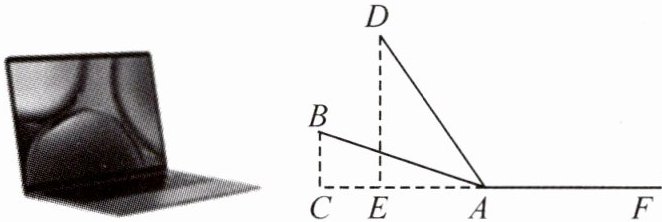
A.15cm
B.18cm
C.21cm
D.24cm

答案： A

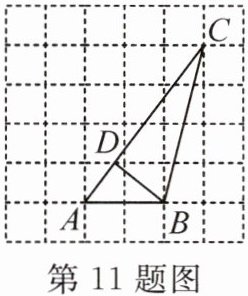
11.如图,网格中每个小正方形的边长为1,则△ABC中边AC上的高BD的长为$\frac{8}{5}$.

答案： $\frac{8}{5}$

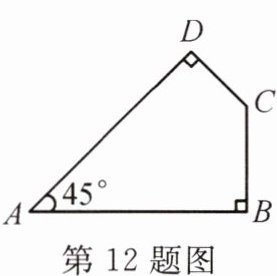
12.如图,在四边形ABCD中,AB=2m,BC=1m,∠A=45°,∠B和∠D都是直角,则四边形ABCD的面积为$\frac{7}{4}$m$^2$.

答案： $\frac{7}{4}$

13.如图,一架云梯AB的长为25米,顶端A靠在墙AC上,此时云梯底端B与墙角C的距离为7米,云梯滑动后停在DE的位置上,测得AE的长为4米,则云梯底端B在水平方向滑动了多少米?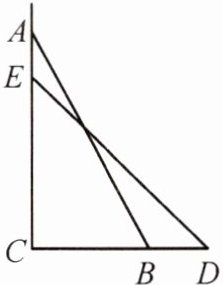

答案： 解：在Rt△ABC中，∠C=90°，AB=25米，BC=7米，
AC=$\sqrt{AB^2 - BC^2}=\sqrt{25^2 - 7^2}=\sqrt{625 - 49}=\sqrt{576}=24$（米）。
∵AE=4米，
∴CE=AC - AE=24 - 4=20（米）。
在Rt△CDE中，∠C=90°，DE=25米，CE=20米，
CD=$\sqrt{DE^2 - CE^2}=\sqrt{25^2 - 20^2}=\sqrt{625 - 400}=\sqrt{225}=15$（米）。
∴BD=CD - BC=15 - 7=8（米）。
答：云梯底端B在水平方向滑动了8米。

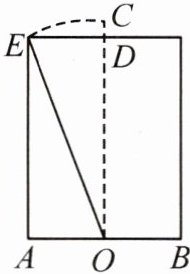
14.《九章算术》卷九“勾股”章中记载:今有池,方一丈,葭生其中央,出水一尺.引葭赴岸,适与岸齐,问水深、葭长各几何.大意如下:如图,水池底面的宽AB=1丈,芦苇OC生长在AB的中点O处,高出水面的部分CD=1尺.将芦苇向池岸牵引,其顶端达到岸边时恰好与水面平齐,即OC=OE,问水池的深度和芦苇的长度各是多少.(1丈=10尺)
(1)求芦苇的长度和水池的深度OD；
(2)中国古代数学家刘徽在为《九章算术》作注解时,进一步地给出了这类问题的一般解法.他的解法用现代符号语言可以表示为:若已知水池宽AB=2a,芦苇高出水面的部分CD=n(n＜a),则水池的深度OD(OD=b)能用含a,n的代数式表示吗?

答案：
(1)设芦苇的长度为$x$尺,
则$OC=OE=x$尺,$OD=(x-1)$尺，
因$O$为$AB$的中点，
所以$AO=\frac{1}{2}AB=5$尺，
$DE=AO=5$尺，
在$Rt\triangle ODE$中, $\angle ODE=90°$，
由勾股定理得：
$DE^2+OD^2=OE^2$，
即$5^2+(x-1)^2=x^2$，
$25+x^2-2x+1=x^2$，
$26-2x=0$，
解得$x=13$，
$OD=13-1=12$尺，
答：芦苇的长度为$13$尺，水池的深度$OD$为$12$尺。
(2)能，
设$OD=b$，$CD=n$，$AB=2a$，
则$OC=OE=b+n$，$DE=a$，
在$Rt\triangle ODE$中, $\angle ODE=90°$，
由勾股定理得：
$DE^2+OD^2=OE^2$，
即$a^2+b^2=(b+n)^2$，
$a^2+b^2=b^2+2bn+n^2$，
$a^2=2bn+n^2$，
$b=\frac{a^2-n^2}{2n}$。