《2025年名校课堂八年级数学上册华师大版》

1. 在△ABC中，∠A，∠B，∠C的对边分别为a，b，c. 若a²=b²+c²，则（A）

A.∠A=90°
B.∠B=90°
C.∠C=90°
D.∠C=∠A+∠B

答案： A

2. 以下列各组数为边长，能组成直角三角形的是（C）

A.2，3，4
B.10，8，4
C.7，25，24
D.7，15，12

答案： C

3. 已知三角形的三边长分别为a，b，c，且满足(a－b)²=c²－2ab，则这个三角形是（C）

A.等边三角形
B.钝角三角形
C.直角三角形
D.锐角三角形

答案： C

4. 如图，小亮家的木门左下角有一点受潮，他想检测门是否变形，准备采用如下方法：先测量门的边AB和BC的长，再测量点A和点C间的距离，由此可推断∠B是否为直角，这样做的依据是（C）

A.勾股定理
B.三角形内角和定理
C.勾股定理的逆定理
D.直角三角形的两锐角互余

答案： C

5. 三角形的三边长分别为6，8，10，则这个三角形的面积是24.

答案： 24

6. 在△ABC中，a，b，c分别是∠A，∠B，∠C的对边长. 若(a－1)²+|b－√5|+√(c－2)=0，则这个三角形一定是直角三角形.

答案： 直角三角形

7. 如图，方格中小正方形的边长均为1，△ABC的三个顶点都在格点（网格线的交点）上. 请判断△ABC是不是直角三角形，并说明理由.

答案： 答题格式如下：
解：△ABC是直角三角形，理由如下：
由方格图可知，各点坐标为$A(2,2),B(5,5),C(5,2)$，
根据两点间距离公式：$d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}$，
$AB = \sqrt{(5 - 2)^2 + (5 - 2)^2} = \sqrt{9 + 9} = \sqrt{18} = 3\sqrt{2}$，
$AC = \sqrt{(5 - 2)^2 + (2 - 2)^2} = \sqrt{9 + 0} = 3$，
$BC = \sqrt{(5 - 5)^2 + (5 - 2)^2} = \sqrt{0 + 9} = 3$，
验证勾股定理：
$AC^2 + BC^2 = 3^2 + 3^2 = 9 + 9 = 18$，
$AB^2 = (3\sqrt{2})^2 = 18$，
因为$AC^2 + BC^2 = AB^2$，
所以△ABC是直角三角形。

8. 如图，在△ABC中，AD⊥BC，AD=12，BD=16，CD=5.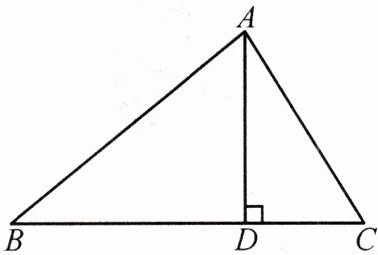

（1）求△ABC的周长；

（2）△ABC是不是直角三角形？为什么？

答案： 解：（1）在Rt△ABD和Rt△ACD中，根据勾股定理，得AB²=AD²+BD²，AC²=AD²+CD².又
∵AD=12，BD=16，CD=5，
∴AB=20，AC=13.
∴△ABC的周长为AB+AC+BC=AB+AC+BD+DC=20+13+16+5=54.（2）△ABC不是直角三角形.理由如下：
∵AB=20，AC=13，BC=21，AB²+AC²≠BC²，
∴△ABC不是直角三角形.

9. 下列各组数中是勾股数的是（D）

A.4，5，6
B.0.3，0.4，0.5
C.1，2，3
D.5，12，13

答案： D

10. （2024·郑州外国语月考）若3，4，a为勾股数，则a的值为（B）

A.√7
B.5
C.5或7
D.5或√7

答案： B