《2025年名校课堂八年级数学上册华师大版》

1.填空：$(a^{2}b^{3})^{4}=(a^{2})^{\underline{}} \cdot ()^{\underline{4}}=a^{2 × \underline{}} \cdot b^{ × }=$

答案： $b^{3}$; 4; 3; 4; $a^{8}b^{12}$

2.(2024·上海)计算：$(4x^{2})^{3}=$64x^{6}$.$

答案： $64x^{6}$

3.(2023·衡阳)计算$\left(\frac{1}{2}x^{3}\right)^{2}$的结果正确的是（）

A.$x^{6}$
B.$\frac{1}{4}x^{6}$
C.$\frac{1}{4}x^{5}$
D.$x^{9}$

答案： B

4.(2024·南阳月考)计算$(-2x^{3}y^{4})^{3}$的结果是（ ）

A.$-6x^{6}y^{7}$
B.$-8x^{27}y^{64}$
C.$-8x^{9}y^{12}$
D.$-6xy^{10}$

答案： C

5.如果$(a^{m}b^{n})^{3}=a^{9}b^{12},$那么m,n的值分别为（ ）
A.9,4
B.3,4
C.4,3
D.9,6

答案： B

6.计算：$(1)(2ab)^{3}；$$(2)(-3x)^{4}；$$(3)(x^{m}y^{n})^{2}；$$(4)(-2×10^{3})^{4}.$

答案： 解:原式$=2^{3}·a^{3}·b^{3}=8a^{3}b^{3}.$解:原式$=(-3)^{4}·x^{4}=81x^{4}.$解:原式$=(x^{m})^{2}·(y^{n})^{2}=x^{2m}y^{2n}.$解:原式$=(-2)^{4}×(10^{3})^{4}=16×10^{12}=1.6×10^{13}.$

7.计算：$3^{7}×\left(\frac{1}{3}\right)^{7}=($3$×$\frac{1}{3}$)^{7}=$1$.$

答案： 3; $\frac{1}{3}$; 1

8.如果$5^{n}=a,4^{n}=b,$那么$20^{n}=$ab$.$

答案： ab

9.计算：$(1)(0.4)^{2025}×\left(\frac{5}{2}\right)^{2025}=$1$；$$(2)(-0.25)^{2024}×4^{2025}=$4$.$

答案： 1; 4

10.(教材P26练习T1变式)指出下列的计算哪些是对的，哪些是错的，并将错误的改正.
(1)$(ab^{2})^{2}=ab^{4};$
(2)$(3cd)^{3}=9c^{3}d^{3};$
(3)$(-3a^{3})^{2}=-9a^{6};(4)(-x^{3}y)^{3}=-x^{6}y^{3}.$

答案： 解:
(1)
(2)
(3)
(4)都是错的.改正如下：$(1)(ab^{2})^{2}=a^{2}b^{4};(2)(3cd)^{3}=27c^{3}d^{3};(3)(-3a^{3})^{2}=9a^{6};(4)(-x^{3}y)^{3}=-x^{9}y^{3}.$

11.下列各图中，能直观解释$“(3a)^{2}=9a^{2}”$的是（ ）

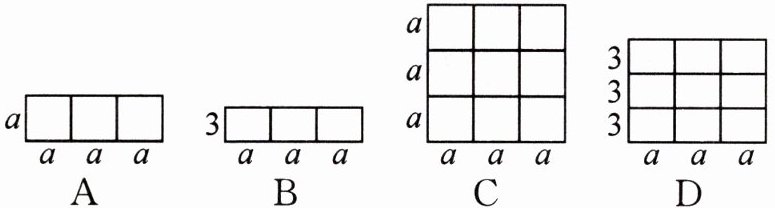
答案： C

12.一个立方体的棱长是$1.5×10^{2}cm,$则这个立方体的体积为$$3.375×10^{6}$cm^{3}.($结果用科学记数法表示)

答案： $3.375×10^{6}$

13.计算：$(1)(-2xy^{2})^{6}+(-3x^{2}y^{4})^{3}；$$(2)\left(-\frac{1}{4}\right)^{2025}×16^{1012}.$

答案： 解:原式$=64x^{6}y^{12}-27x^{6}y^{12}=37x^{6}y^{12}.$解:原式$=-\frac{1}{4}×\left(-\frac{1}{4}\right)^{2024}×4^{2024}=-\frac{1}{4}×\left(-\frac{1}{4}×4\right)^{2024}=-\frac{1}{4}.$

14.新考向 推理能力 已知$2^{n}=a,3^{n}=b,12^{n}=c,$试探究a,b,c之间满足的等量关系.
解:∵$12^{n}=(2^{2}×3)^{n}=2^{2n}×3^{n}=(2^{n})^{2}×3^{n}=a^{2}b,$且$12^{n}=c,$∴$a^{2}b=c.$

答案： 解:
∵$12^{n}=(2^{2}×3)^{n}=2^{2n}×3^{n}=(2^{n})^{2}×3^{n}=a^{2}b,$且$12^{n}=c,$
∴$a^{2}b=c.$