《2025年初中同步学习导与练导学探究案八年级数学上册人教版》

1. 以虚线为对称轴,将虚线右边和下边的部分补充完整,看它表示什么？

答案：

2. 观察下列图案：

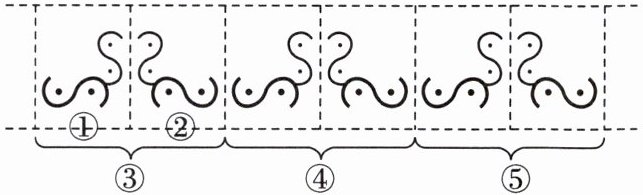
图①到②是利用轴对称得到的,图③经过平移或轴对称都可以直接得到图④；上面图案设计说明,有时需将轴对称和平移结合起来设计图案。

答案： 轴对称 平移 轴对称 轴对称 平移

3. 请从如图(1)所示的两种瓷砖中各选2块,拼成一个新的正方形地板图案,使拼成的图案是轴对称图形[如图(2)所示]。要求：分别在图(3)、图(4)中各设计一种与图(2)不同的拼法的轴对称图形。

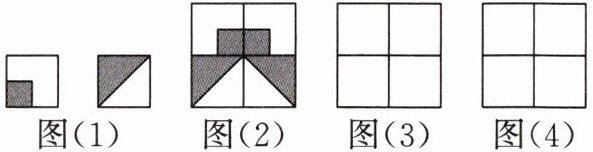
答案：

4. 项目式学习
项目主题：探索等腰三角形中相等的线段。
项目情境：数学活动课上,老师提出了一个问题：等腰三角形底边中点到两腰的距离相等吗？同学们就这个问题展开探究。
(1)项目初探：希望小组的同学根据题意画出了相应的图形,如图(1)所示,在△ABC中,AB= AC,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别为点E,F。经过合作,该小组的同学得出的结论是DE= DF。请你帮希望小组说明结论成立的理由；
(2)类比探究：奋斗小组的同学认真研究过后,发现了以下两个正确结论：
①在图(2)中,若DE,DF分别为△ABD和△ACD的中线,那么DE= DF仍然成立；
②在图(3)中,若DE,DF分别为△ABD和△ACD的角平分线,那么DE= DF仍然成立。
请你选择其中一个结论,写出证明过程。

答案： 解:
(1)
∵DE⊥AB,DF⊥AC,
∴∠DEB=∠DFC=90°.
∵AB=AC,
∴∠B=∠C.
∵D 是 BC 的中点,
∴BD=CD.
在△BDE 和△CDF 中,
∠DEB=∠DFC,
∠B=∠C,
BD=CD,
∴△BDE≌△CDF(AAS).
∴DE=DF.
(2)(答案不唯一)选择①.证明:
∵DE,DF 是△ABD 和△ACD 的中线,
∴BE=1/2AB,CF=1/2AC.
∵AB=AC,
∴BE=CF,∠B=∠C.
又
∵D 是 BC 的中点,
∴BD=CD.
在△BDE 与△CDF 中,
BE=CF,
∠B=∠C,
DB=CD,
∴△BDE≌△CDF(SAS),
∴DE=DF.