第45页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
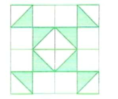
1. 如图所示,仔细观察图案,图中有几对全等形?有几对全等三角形?你能否举一些生活中利用全等设计图案的例子?


答案:
1. 解:
全等形:
观察图案,通过平移、旋转、对称等变换可以发现,图中有$4$对全等形。
全等三角形:
图中有$2$对全等三角形。
生活中利用全等设计图案的例子:
比如一些地砖的铺设(正方形地砖等,它们的形状和大小都相同,是全等形);一些装饰图案(如由全等的菱形组成的装饰图案等)。
综上,图中有$4$对全等形,$2$对全等三角形。
全等形:
观察图案,通过平移、旋转、对称等变换可以发现,图中有$4$对全等形。
全等三角形:
图中有$2$对全等三角形。
生活中利用全等设计图案的例子:
比如一些地砖的铺设(正方形地砖等,它们的形状和大小都相同,是全等形);一些装饰图案(如由全等的菱形组成的装饰图案等)。
综上,图中有$4$对全等形,$2$对全等三角形。
2. 请用 为基本图案,在下面的方格中设计一个美丽的图案。
为基本图案,在下面的方格中设计一个美丽的图案。
 为基本图案,在下面的方格中设计一个美丽的图案。
为基本图案,在下面的方格中设计一个美丽的图案。
答案:

3. 如图所示,下面的图案分别是由若干个全等的基本图案拼成的。请你找出这个基本图案并画出来,再仿照此方法设计一个美丽的图案。
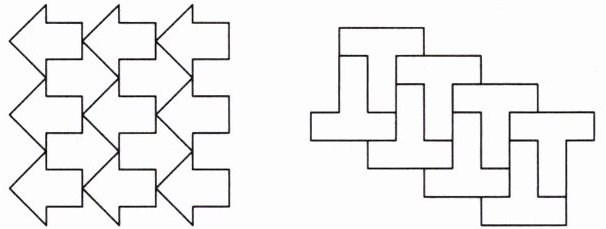

答案:
基本图形:

设计的图案: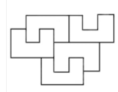
基本图形:


设计的图案:

4. 如图所示,艳艳剪了一个燕尾图案,她用刻度尺量得 $ AB = AC $,$ BO = CO $,为了保证图案的美观,她准备再用量角器量一下 $ \angle B $ 与 $ \angle C $ 是否相等,小麦走过来说:“不用量了,一定相等。”你认为小麦的说法
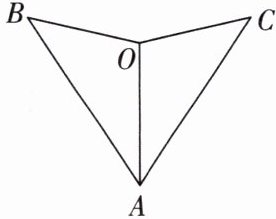
正确
。(填“正确”或“错误”)
答案:
正确
5. 如图所示,请用 4 个如图(1)所示的小“L”形纸片拼成一个与如图(2)所示的大“L”形纸片全等的图案。
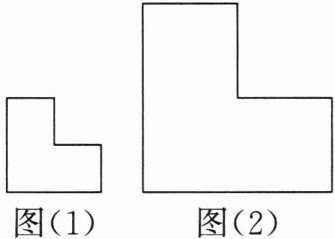

答案:
解:如图所示:

解:如图所示:

6. 如图所示,已知 $ \triangle ABD \cong \triangle CDB $,点 $ O $ 是 $ AC $ 与 $ BD $ 的交点,过点 $ O $ 的直线分别交 $ AD $,$ BC $ 于点 $ E $,$ F $。$ OE $ 与 $ OF $ 有怎样的数量关系?请说明理由。


答案:
解:OE=OF.理由如下:
∵△ABD≌△CDB,
∴∠ADB=∠CBD,AD=CB.
在△AOD和△COB中,
∠ADB=∠CBD,
∠AOD=∠COB,
AD=CB,
∴△AOD≌△COB(AAS).
∴OD=OB.
在△ODE和△OBF中,
∠EDO=∠FBO,
OD=OB,
∠DOE=∠BOF,
∴△ODE≌△OBF(ASA).
∴OE=OF.
∵△ABD≌△CDB,
∴∠ADB=∠CBD,AD=CB.
在△AOD和△COB中,
∠ADB=∠CBD,
∠AOD=∠COB,
AD=CB,
∴△AOD≌△COB(AAS).
∴OD=OB.
在△ODE和△OBF中,
∠EDO=∠FBO,
OD=OB,
∠DOE=∠BOF,
∴△ODE≌△OBF(ASA).
∴OE=OF.
查看更多完整答案,请扫码查看


