第27页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
7. 如图所示,AD是△ABC的角平分线,CE⊥AD,垂足为F. 若∠CAB= 30°,∠B= 55°,则∠BDE的度数为(

A.35°
B.40°
C.45°
D.50°
B
)
A.35°
B.40°
C.45°
D.50°
答案:
B
8. 一名工作人员不慎将一块三角形模具打碎成了如图所示的四块,他需要去商店再配一块与原来大小和形状完全相同的模具. 现只能拿着两块去配,其中不能配出符合要求的模具的是(

A.①②
B.②④
C.①④
D.②③
C
)
A.①②
B.②④
C.①④
D.②③
答案:
C
9. 如图所示,在四边形ABCD中,AB//DC,E为BC的中点,连接DE,AE,AE⊥DE. 若AB= 6,CD= 4,则AD的长为(
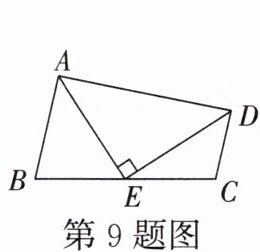
A.11
B.10
C.5
D.2
B
)
A.11
B.10
C.5
D.2
答案:
B
10. 如图所示,∠E= ∠F= 90°,∠B= ∠C,AE= AF,有以下结论:①EM= FN;②CD= DN;③∠FAN= ∠EAM;④△ACN≌△ABM. 其中正确的结论是
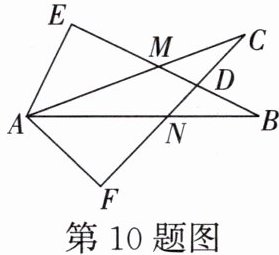
①③④
(填序号).
答案:
①③④
11. 在等腰直角三角形ABC中,∠BAC= 90°,AB= AC,点A,B分别是y轴、x轴上的两个动点,直角边AC交x轴于点D,斜边BC交y轴于点E.(提示:等腰三角形的两个底角相等)
(1)如图(1)所示,已知点C的横坐标为-1,直接写出点A的坐标;

(2)如图(2)所示,当等腰直角三角形ABC运动到点D恰好为AC的中点时,连接DE,求证:∠ADB= ∠CDE.
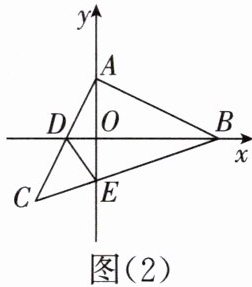
(1)如图(1)所示,已知点C的横坐标为-1,直接写出点A的坐标;

(2)如图(2)所示,当等腰直角三角形ABC运动到点D恰好为AC的中点时,连接DE,求证:∠ADB= ∠CDE.

答案:
(1)解:点A的坐标为(0,1).
(2)证明:如图所示,过点C作CG⊥AC交y轴于点G.
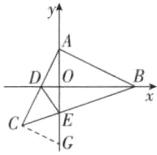
∵CG⊥AC,
∴∠ACG=90°,
∴∠CAG+∠AGC=90°.
∵∠AOD=90°,
∴∠ADO+∠DAO=90°,
∴∠AGC=∠ADO.
在△ACG和△BAD中,
∠ACG=∠BAD=90°,
∠AGC=∠BDA,
AC=BA,
∴△ACG≌△BAD(AAS),
∴CG=AD=CD.
∵∠CAB=90°,AC=AB,
∴∠ACB=∠ABC=45°.
∵∠ACB=45°,∠ACG=90°,
∴∠DCE=∠GCE=45°.
在△DCE和△GCE中,
CD=CG,
∠DCE=∠GCE,
CE=CE,
∴△DCE≌△GCE(SAS),
∴∠CDE=∠AGC,
∴∠ADB=∠CDE.
(1)解:点A的坐标为(0,1).
(2)证明:如图所示,过点C作CG⊥AC交y轴于点G.

∵CG⊥AC,
∴∠ACG=90°,
∴∠CAG+∠AGC=90°.
∵∠AOD=90°,
∴∠ADO+∠DAO=90°,
∴∠AGC=∠ADO.
在△ACG和△BAD中,
∠ACG=∠BAD=90°,
∠AGC=∠BDA,
AC=BA,
∴△ACG≌△BAD(AAS),
∴CG=AD=CD.
∵∠CAB=90°,AC=AB,
∴∠ACB=∠ABC=45°.
∵∠ACB=45°,∠ACG=90°,
∴∠DCE=∠GCE=45°.
在△DCE和△GCE中,
CD=CG,
∠DCE=∠GCE,
CE=CE,
∴△DCE≌△GCE(SAS),
∴∠CDE=∠AGC,
∴∠ADB=∠CDE.
查看更多完整答案,请扫码查看


