《2025年超越训练七年级数学上册人教版四川专版》

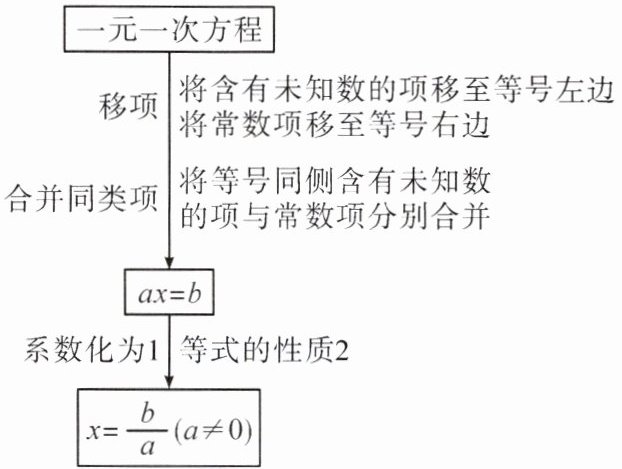
1. 利用移项解一元一次方程的步骤：

一元一次方程
移项：将含有未知数的项移至等号左边，将常数项移至等号右边
合并同类项：将等号同侧含有未知数的项与常数项分别合并
得到 $ax = b$
系数化为 1（等式的性质 2）：得到 $x=\frac{b}{a}(a\neq0)$
2. 移项时将某一项从方程的一边移至另一边，注意原项的符号要改变，即“+”变“-”，“-”变“+”，简记为“过等号变符号，不过等号不变号”。

答案：
1. 利用移项解一元一次方程的步骤：

一元一次方程
移项：将含有未知数的项移至等号左边，将常数项移至等号右边
合并同类项：将等号同侧含有未知数的项与常数项分别合并
得到 $ax = b$
系数化为 1（等式的性质 2）：得到 $x=\frac{b}{a}(a\neq0)$
2. 移项时将某一项从方程的一边移至另一边，注意原项的符号要改变，即“+”变“-”，“-”变“+”，简记为“过等号变符号，不过等号不变号”。

例 1 解下列方程：
(1) $2x + 7 = 5x - 14$；
(2) $x + \frac{1}{6} - \frac{1}{6}x = 5 - \frac{1}{3}x - 3$。
解题策略：将方程中的某一项改变符号后，从方程的一边移到另一边叫作移项；在同一边改变某一项的位置不是移项，因此它的符号不发生变化。

答案： 例1 解：
(1)移项，得2x - 5x = -14 - 7，合并同类项，得-3x = -21，系数化为1，得x = 7。
(2)移项，得$x - \frac{1}{6}x + \frac{1}{3}x = 5 - 3 - \frac{1}{6}，$合并同类项，得$\frac{7}{6}x = \frac{11}{6}，$系数化为1，得$x = \frac{11}{7}。$

例 2 某单位中秋节给员工发苹果。若每人分 2 箱，则剩余 20 箱；若每人分 3 箱，则还缺 20 箱。苹果有多少箱？
解题策略：本题有两种解法：①设直接未知数，利用人数的两种不同表示方法列方程；②设间接未知数，利用苹果数量的两种不同表示方法列方程。

答案： 例2 解：设员工有x人。由题意，得2x + 20 = 3x - 20，解得x = 40，所以2x + 20 = 100。答：苹果有100箱。

1. 解下列方程：
(1) $3x + \frac{5}{2} = x - \frac{3}{2}$；
(2) $\frac{4}{3} - \frac{3}{4}x = x - 3\frac{1}{3}$。

答案： 1.
(1)解：x = -2。
(2)解：$x = \frac{8}{3}。$

2. 甲厂库存钢材 100 t，每月用去 15 t；乙厂库存钢材 82 t，每月用去 9 t。经过3个月后，两厂剩下的钢材相等。

答案： 2.3

3. 某中学七年级(1)班全体学生参加义务植树活动。如果每人种 6 棵树，那么剩余 15 棵树苗；如果每人种 7 棵树，那么还差 33 棵树苗。这个班共有多少名学生？共有多少棵树苗？

答案： 3.解：设这个班共有x名学生。由题意，得6x + 15 = 7x - 33，解得x = 48，所以6x + 15 = 6×48 + 15 = 303。答：这个班共有48名学生，共有303棵树苗。