《2025年超越训练七年级数学上册人教版四川专版》

9. 用小木棍按如图所示的规律搭三角形，则搭$n$个三角形需要(2n + 1)根小木棍.

答案： 9.(2n + 1)

10. 如图，一个花坛由两个半圆和一个长方形组成.若长方形的长为$a m$，宽为$2b m$，则该花坛的周长为(2a + 2\pi b)$m$，面积为(2ab+\pi b^{2})$m^{2}$.

答案： $10.(2a + 2\pi b)(2ab+\pi b^{2})$

11. 一根弹簧长$12cm$，在弹性限度(总长不超过$20cm$)内，每挂质量为$1kg$的物体，弹簧伸长$0.5cm$.
(1)代数式$0.5x + 12$表示的实际意义是挂上质量为xkg的物体后，弹簧的总长度.
(2)这根弹簧最多可挂质量为多少千克的物体?

答案： 11.解：
(1)挂上质量为xkg的物体后，弹簧的总长度.
(2)设这根弹簧最多可挂质量为ykg的物体.由题意，得0.5y + 12 = 20，解得y = 16.答：这根弹簧最多可挂质量为16kg的物体.

12. 某地出租车的收费标准是：$3km$以内(包括$3km$)为起步价收 8 元，超过$3km$以后的价格为$2$元/km.
(1)若某人乘坐出租车行驶的路程为$2.9km$，则应收费8元.
(2)若某人乘坐出租车行驶的路程为$7km$，则应收费16元.
(3)若某人乘坐出租车行驶的路程为$x km(x＞3)$，求应收费多少元(用含$x$的式子表示).

答案： 12.解：
(1)8.
(2)16.
(3)若某人乘坐出租车行驶的路程为xkm(x＞3)，则应收费[8 + 2(x - 3)]元.

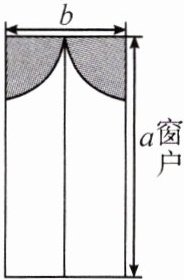
13. 小安房间窗户的装饰物(不透光)如图所示(阴影部分)，它由两个四分之一圆组成(半径相同).
(1)若$\vert a - 2\vert+(b - 1)^{2}=0$，求$a$，$b$的值；
(2)利用(1)中数据(单位：m)求出窗户能射进阳光的面积($\pi$取 3).

答案： 13.解：
(1)因为$\vert a - 2\vert+(b - 1)^{2}=0，$所以a - 2 = 0，b - 1 = 0，解得a = 2，b = 1.
(2)窗户能射进阳光的面积为$ab-\pi\cdot(\frac{b}{2})^{2}×\frac{1}{2}=2×1 - 3×(\frac{1}{2})^{2}×\frac{1}{2}=2×1 - 3×\frac{1}{4}×\frac{1}{2}=2-\frac{3}{8}=\frac{13}{8}(m^{2}).$答：窗户能射进阳光的面积为$\frac{13}{8}m^{2}.$

14. 某市一企业今年 8 月份的产值为$m$万元，9 月份的产值比 8 月份减少了$5\%$，10 月份的产值比 9 月份增加了$10\%$，则 10 月份的产值为(D)

A.$(m + 5\%)(m - 10\%)$万元
B.$(m - 5\%)(m + 10\%)$万元
C.$(1 + 5\%)(1 - 10\%)m$万元
D.$(1 - 5\%)(1 + 10\%)m$万元

答案： 14.D

15. 逻辑推理下列图案是由火柴棒按规律拼成的，第 1 个图案中有 2 个正方形，第 2 个图案中有 5 个正方形，第 3 个图案中有 8 个正方形……

(1)第 5 个图案中有14个正方形.
(2)第$n$个图案中有(3n - 1)个正方形.
(3)按此规律拼成的图案中，正方形的个数能否为 2025? 为什么?

答案： 15.解：
(1)14.
(2)(3n - 1).
(3)由3n - 1 = 2025，解得$n=\frac{2026}{3}=675\frac{1}{3}.$因为n的值不为整数，所以正方形的个数不能为2025.