《2025年超越训练七年级数学上册人教版四川专版》

5. 一列火车从丙站开往甲站，发车时车上有乘客$(288m - 16n)$人，经乙站时，有$\frac{3}{4}$的乘客下车了，同时又有一部分乘客上车，这时车上共有乘客$(104m - 24n)$人。
（1）从乙站上车的乘客有多少人（用含$m$，$n$的式子表示）？
（2）当$m = 8$，$n = 5$时，求从乙站上车的乘客人数。

答案： 5.解：
(1)$104m - 24n - (1 - \frac{3}{4})(288m - 16n) = [104m - 24n - \frac{1}{4}(288m - 16n)]$（人），所以从乙站上车的乘客有$[104m - 24n - \frac{1}{4}(288m - 16n)]$人。
(2)当$m = 8$，$n = 5$时，原式$= 104 × 8 - 24 × 5 - \frac{1}{4} × (288 × 8 - 16 × 5) = 156$（人），所以从乙站上车的乘客有156人。

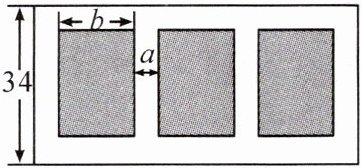
6. 如图，某学校计划在宽为$34 m$的大长方形场地中，并排新建三个大小相同的篮球场，三个篮球场之间及篮球场与长方形场地边沿的距离均为$a m$，篮球场的宽为$b m$。（图中单位：$m$）
（1）用含$a$，$b$的代数式表示一个篮球场的周长；
（2）若$|a - 6| + (b - 16)^2 = 0$，求整个长方形场地的面积。

答案： 6.解：
(1)篮球场的长为$(34 - 2a)m$，一个篮球场的周长为$2(34 - 2a + b)m$。
(2)因为$|a - 6| + (b - 16)^2 = 0$，所以$a - 6 = 0$，$b - 16 = 0$，所以$a = 6$，$b = 16$。整个长方形场地的面积为$34(4a + 3b)m^2$。当$a = 6$，$b = 16$时，$34(4a + 3b) = 34 × (4 × 6 + 3 × 16) = 2448$，即整个长方形场地的面积为$2448m^2$。

7. 某超市的某件商品近期进行了两次调价，第一次提价$30\%$，第二次在第一次的基础上降价$30\%$。
（1）若该商品在调价前售价为$x$元，则第一次、第二次调价后的售价分别是多少元？
（2）现该超市搞优惠促销活动：购物每满$100$元减$10$元。若$x = 210$，则在两次调价后，小明只买一件该商品应付多少钱？

答案： 7.解：
(1)第一次调价后的售价为$x × (1 + 30\%) = 1.3x$（元）。第二次调价后的售价为$1.3x × (1 - 30\%) = 0.91x$（元）。
(2)当$x = 210$时，$0.91x = 0.91 × 210 = 191.1$（元）。因为购物每满100元减10元，所以$191.1 - 10 = 181.1$（元）。答：小明只买一件该商品应付181.1元。

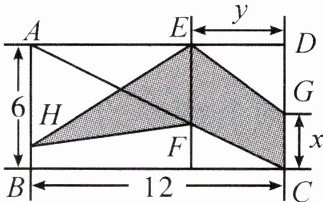
8. [教材例题变式]如图，两个长方形拼成了一个大长方形，大长方形的对角线$AC$与拼接线相交于点$F$。
（1）用含$x$，$y$的代数式表示图中阴影部分的面积$S$；
（2）当$x = 2$，$y = 3$时，求阴影部分的面积。

答案： 8.解：
(1)易得三角形$EFH$与三角形$EFA$的面积相等，所以$S = S_{三角形ACD} - S_{三角形EDG} = \frac{1}{2} × 6 × 12 - \frac{1}{2}y(6 - x) = 36 - \frac{1}{2}y(6 - x)$。
(2)当$x = 2$，$y = 3$时，$S = 36 - \frac{1}{2} × 3 × (6 - 2) = 30$。