《2025年超越训练七年级数学上册人教版四川专版》

8. 有 20 筐白萝卜，以每筐 20 kg 为质量标准，把每筐白萝卜超过 20 kg 的千克数记作正数，不足的千克数记作负数，记录如下表：

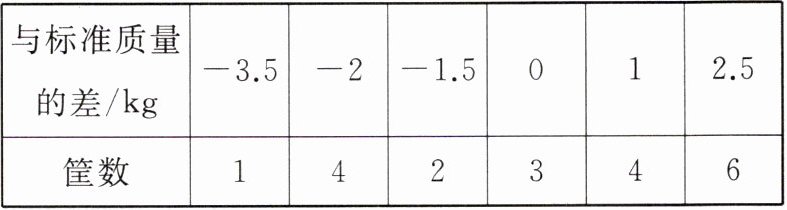
(1)这 20 筐白萝卜中，最重的一筐比最轻的一筐重6kg.
(2)与标准质量相比，这 20 筐白萝卜总计超过(或不足)多少千克？
(3)若白萝卜每千克的售价为 2 元，售出这 20 筐白萝卜可得多少元？

答案： 8.解：
(1)6.
(2)$-3.5×1+(-2)×4+(-1.5)×2+0×3+1×4+2.5×6=4.5(kg)$.答：这20筐白萝卜总计超过标准质量4.5kg.
(3)20筐白萝卜的总质量为$20×20 + 4.5=404.5(kg)$，总售价为$404.5×2 = 809$（元）.答：售出这20筐白萝卜可得809元.

9. 逻辑推理 小明写出一组数：$ \frac{2}{5} $，$ \frac{4}{7} $，$ \frac{8}{11} $，$ \frac{16}{19} $，$ \frac{32}{35} $，…小亮猜出第 6 个数是 $ \frac{64}{67} $.根据此规律，第 $ n $ 个数是$\frac{2^{n}}{2^{n}+3}$.

答案： 9.$\frac{2^{n}}{2^{n}+3}$

10. 逻辑推理 (1)计算 $ \frac{1}{2} + \frac{1}{6} + \frac{1}{12} + \frac{1}{20} + \frac{1}{30} + \cdots + \frac{1}{9900} $ 的结果为$\frac{99}{100}$.
(2)观察下列各式：$ 1^3 = 1^2 $，$ 1^3 + 2^3 = 3^2 $，$ 1^3 + 2^3 + 3^3 = 6^2 $，$ 1^3 + 2^3 + 3^3 + 4^3 = 10^2 $，…计算 $ 1^3 + 2^3 + 3^3 + \cdots + 10^3 $ 的结果是3025.

答案： 10.
(1)$\frac{99}{100}$
(2)3025

11. 逻辑推理 观察下列运算：$ 7^1 = 7 $，$ 7^2 = 49 $，$ 7^3 = 343 $，$ 7^4 = 2401 $，$ 7^5 = 16807 $，$ 7^6 = 117649 $，…则 $ 7^1 + 7^2 + 7^3 + 7^4 + \cdots + 7^{2025} $ 的和的个位数字是7.

答案： 11.7

12. [教材例题变式]观察下面三行数.
第一行：1，4，9，16，25，…；
第二行：0，- 3，- 8，- 15，- 24，…；
第三行：$ \frac{1}{2} $，$ - \frac{2}{3} $，$ \frac{3}{10} $，$ - \frac{4}{15} $，$ \frac{5}{26} $，…
（1）第一行中的数是按什么规律排列的？第二行中的数与第一行中的数有什么关系？
（2）按第三行中的数的排列规律，第 9 个数和第 10 个数分别是多少？第 $ n $ 个数呢？
（3）取每行中的第 20 个数，计算这三个数的和.

答案： 12.解：
(1)第一行中的数的排列规律为$1^{2}$，$2^{2}$，$3^{2}$，$4^{2}$，$5^{2}$，$\cdots$.第二行中的数是第一行中相应的数减1，再取差的相反数，即$-(1^{2}-1)$，$-(2^{2}-1)$，$-(3^{2}-1)$，$-(4^{2}-1)$，$-(5^{2}-1)$，$\cdots$.
(2)第9个数和第10个数分别是$\frac{9}{82}$，$-\frac{10}{99}$.当$n$为奇数时，第$n$个数为$\frac{n}{n^{2}+1}$；当$n$为偶数时，第$n$个数为$-\frac{n}{n^{2}-1}$.
(3)$20^{2}+[-(20^{2}-1)]+(-\frac{20}{20^{2}-1})=\frac{379}{399}$.

13. 我国的港珠澳大桥是世界上最长的跨海大桥，桥隧全长 55 km，工程项目总投资 1269 亿元.将 1269 亿用科学记数法表示为$1.269×10^{11}$.

答案： 13.$1.269×10^{11}$

14. 有下列说法：① 0.750 精确到百分位；② $ 3.079 × 10^4 $ 精确到千分位；③ 38 万精确到个位；④ $ 2.80 × 10^5 $ 精确到千位.其中正确的是④(填序号).

答案： 14.④

15. 近似数 2.0 的准确值 $ a $ 的取值范围是$1.95\leq a＜2.05$.

答案： 15.$1.95\leq a＜2.05$