《2025年超越训练七年级数学上册人教版四川专版》

6. 数学文化 程大位的《直指算法统宗》里记载了这样一道趣题：一百馒头一百僧，大僧三个更无争，小僧三人分一个，大小和尚各几丁？意思是：有 $ 100 $ 个和尚分 $ 100 $ 个馒头，如果大和尚 $ 1 $ 人分 $ 3 $ 个，小和尚 $ 3 $ 人分 $ 1 $ 个，正好分完，试问大、小和尚各多少人？设大和尚有 $ x $ 人，由题意可列方程为(C)

A.$ \frac{x}{3} + 3(100 - x) = 100 $
B.$ \frac{x}{3} - 3(100 - x) = 100 $
C.$ 3x + \frac{100 - x}{3} = 100 $
D.$ 3x - \frac{100 - x}{3} = 100 $

答案： 6.C

7. 数学文化 《增删算法统宗》里有这样一首古算诗：林下牧童闹如簇，不知人数不知竹.每人六竿多十四，每人八竿恰齐足.其大意是：牧童们在树下拿着竹竿玩耍，不知有多少人和竹竿，每人分 $ 6 $ 竿，多 $ 14 $ 竿；每人分 $ 8 $ 竿，恰好用完.则牧童有7人，竹竿有56根.

答案： 7.7 56

8. 我们知道，无限循环小数都可以转化为分数，例如 $ 0.\dot{3} $ 转化为分数时，可设 $ 0.\dot{3} = x $，则 $ 3.\dot{3} = 10x $，两式相减可得 $ 3 = 9x $，解得 $ x = \frac{1}{3} $，即 $ 0.\dot{3} = \frac{1}{3} $.仿此方法，将 $ 1.\dot{4}\dot{5} $ 化成分数是\frac{16}{11}.

答案： $8.\frac{16}{11}$

9. 逻辑推理 有一列按照规律排列的 $ n $ 个数：$ 1, -2, 4, -8, 16, -32, 64, \cdots $.如果最后两个数的差为 $ -1536 $，那么 $ n $ 的值为11.

答案： 9.11

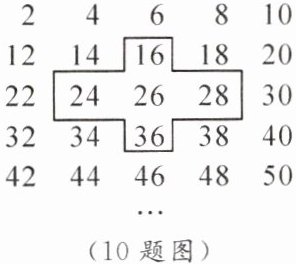
10. 逻辑推理 将连续的偶数 $ 2, 4, 6, 8, 10, \cdots $ 排列成如图所示的数表，现将图中的十字框上下左右平移，若框住的 $ 5 $ 个数字之和是 $ 330 $，则框中最小的数是56.


]

答案： 10.56

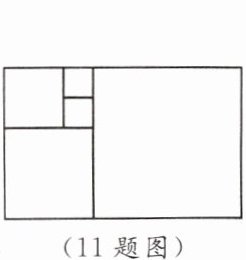
11. 如图，一个长方形内部能用一些正方形铺满，既不重叠，又无缝隙.若长方形的周长为 $ 26 \, cm $，则最右边正方形的边长为5 $ cm $.

答案： 11.5

12. 已知小明和爸爸今年的年龄和为 $ 36 $ 岁，$ 5 $ 年后爸爸的年龄比小明年龄的 $ 4 $ 倍还大 $ 1 $ 岁.当爸爸 $ 40 $ 岁时，小明多少岁？

答案： 12.解：设小明今年x岁，则爸爸今年(36 - x)岁.由题意，得(36 - x) + 5 = 4(x + 5) + 1，解得x = 4，所以36 - x = 32.小明和爸爸的年龄相差32 - 4 = 28(岁)，所以40 - 28 = 12(岁).答：当爸爸40岁时，小明12岁.

13. 一套仪器由 $ 1 $ 个 $ A $ 部件和 $ 3 $ 个 $ B $ 部件构成.用 $ 1 \, m^3 $ 钢材可做 $ 40 $ 个 $ A $ 部件或 $ 240 $ 个 $ B $ 部件.现在用 $ 6 \, m^3 $ 钢材制作这种仪器，应用多少钢材做 $ A $ 部件，多少钢材做 $ B $ 部件，才能恰好配成成套的这种仪器？能配多少套这种仪器？

答案： 13.解：设用x m³钢材做A部件，则用(6 - x)m³钢材做B部件.由题意，得240(6 - x) = 3×40x，解得x = 4，所以6 - x = 2，40x = 160.答：用4m³钢材做A部件，2m³钢材做B部件，才能恰好配成成套的这种仪器，能配160套.

14. 一列客车长 $ 190 \, m $，一列货车长 $ 290 \, m $，客车与货车的速度之比为 $ 5:3 $.已知它们相向行驶时，两车错车时间为 $ 10 \, s $，求两车的速度.

答案： 14.解：设客车、货车的速度分别为5x m/s，3x m/s.由题意，得10×5x + 10×3x = 190 + 290，解得x = 6，所以5x = 30，3x = 18.答：客车、货车的速度分别为30m/s，18m/s.