《2025年超越训练七年级数学上册人教版四川专版》

用数值代替代数式中的字母，按照代数式中的运算关系计算得出的结果，叫作代数式的值。
列代数式$\xrightarrow{用数值代替字母}$按运算关系计算$\to$代数式的值。

答案： 无（题目未要求具体计算或选择，仅为概念陈述）

例 1 解答下列问题。
（1）根据下列$a$，$b$的值，分别求代数式$(a - b)^2$和$a^2 - 2ab + b^2$的值。
①$a = 2$，$b = - 3$；②$a = - \frac{2}{3}$，$b = - \frac{3}{2}$。
（2）根据（1）中的计算，你有什么猜想？

答案：
(1)解：①当$a = 2$，$b = -3$时，$(a - b)^2 = [2 - (-3)]^2 = 5^2 = 25$，$a^2 - 2ab + b^2 = 2^2 - 2 × 2 × (-3) + (-3)^2 = 25$。②当$a = -\frac{2}{3}$，$b = -\frac{3}{2}$时，$(a - b)^2 = [(-\frac{2}{3}) - (-\frac{3}{2})]^2 = (\frac{5}{6})^2 = \frac{25}{36}$，$a^2 - 2ab + b^2 = (-\frac{2}{3})^2 - 2 × (-\frac{2}{3}) × (-\frac{3}{2}) + (-\frac{3}{2})^2 = \frac{25}{36}$。
(2)解：由
(1)中的计算猜想$(a - b)^2 = a^2 - 2ab + b^2$。

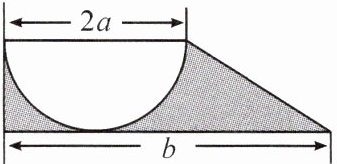
例 2 如图，工人师傅用一块直角梯形的铁皮，剪裁出一块半圆形铁件。
（1）用代数式表示剩余铁皮的面积$S$；
（2）若$a = \frac{39}{10}cm$，$b = 14cm$，求剩余铁皮的面积（$\pi$取$3.14$，结果精确到$0.1$）。

答案： 解：
(1)$S = \frac{1}{2}(2a + b)a - \frac{1}{2}\pi a^2$。
(2)当$a = \frac{39}{10} cm$，$b = 14 cm$时，$S = \frac{1}{2} × (2 × \frac{39}{10} + 14) × \frac{39}{10} - \frac{1}{2} × 3.14 × (\frac{39}{10})^2 \approx 18.6 (cm^2)$。

1. (1)若$x = 2$，则代数式$\frac{1}{3}x - 1$的值是$-\frac{1}{3}$；
(2)若$x = - \frac{1}{3}$，则代数式$2x^2 - 5x$的值是$\frac{17}{9}$。

答案： 1.
(1)$-\frac{1}{3}$
(2)$\frac{17}{9}$

2. 已知$|a| = | - 3|$，则代数式$a^2 - 2a + 1$的值是4或16。

答案： 2.4或16

3. 已知$|a + 2| + |b - 3| = 0$，则代数式$\frac{a^2 - b^2}{a + b}$的值是-5。

答案： 3.-5

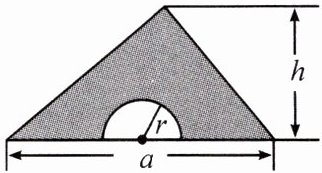
4. [教材例题变式]如图，在一个底为$a$，高为$h$的三角形铁皮上剪去一个半径为$r$的半圆。
（1）用含$a$，$h$，$r$的代数式表示剩下铁皮（阴影部分）的面积$S$；
（2）当$a = 10$，$h = 4.8$，$r = \frac{3}{2}$时，求$S$的值（$\pi$取$3.14$，结果精确到百分位）。

答案： 4.解：
(1)$S = \frac{1}{2}ah - \frac{1}{2}\pi r^2$。
(2)当$a = 10$，$h = 4.8$，$r = \frac{3}{2}$时，$S = \frac{1}{2} × 10 × 4.8 - \frac{1}{2} × 3.14 × (\frac{3}{2})^2 \approx 20.47$。