《2025年超越训练七年级数学上册人教版四川专版》

3. 由五个完全相同的小长方形拼成的大长方形如图所示. 若大长方形的周长是 32 cm，则每个小长方形的面积为12 cm².

答案： 3.12

4. 如图，用 A，B 两种规格的长方形纸板无重合、无缝隙地拼接成一个周长为 32 cm 的正方形. 已知 A 种长方形的宽为 1 cm，则 B 种长方形的面积为12 cm².

答案： 4.12

1. 爷孙俩共下 12 局棋(未出现和棋)后，得分相同，爷爷赢一局得 1 分，孙子赢一局得 2 分，那么爷爷赢了(B)

A.9 局
B.8 局
C.4 局
D.3 局

答案： 1.B

2. 在足球联赛的前 11 轮比赛中，某队保持不败，共得 23 分，按比赛规则胜一场得 3 分，平一场得 1 分，则该队胜了(C)

A.4 场
B.5 场
C.6 场
D.7 场

答案： 2.C

3. 在“人与自然”知识竞赛中，竞赛试题共有 25 道，每道题都给出四个答案，其中只有一个答案正确. 每道题选对得 4 分，不选或选错倒扣 2 分. 如果一名学生在本次竞赛中的得分不低于 60 分，那么这名学生至少应选对的题数是(C)

A.17
B.18
C.19
D.20

答案： 3.C

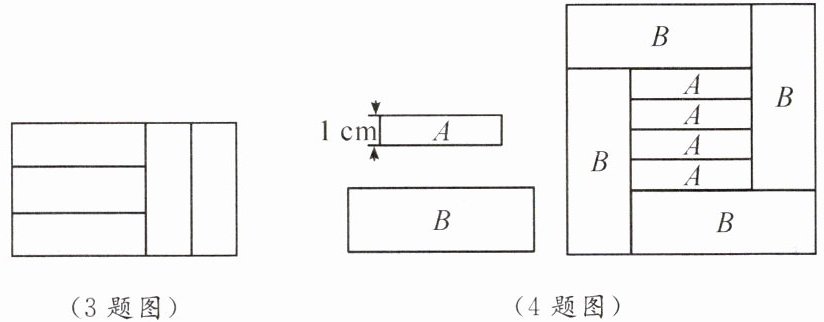
4. 按如图所示的信息，可列方程为(A)


A.$ \pi × \left( \dfrac{8}{2} \right)^2 x = \pi × \left( \dfrac{6}{2} \right)^2 × (x + 5) $
B.$ \pi × \left( \dfrac{8}{2} \right)^2 x = \pi × \left( \dfrac{6}{2} \right)^2 × (x - 5) $
C.$ \pi × 8^2 x = \pi × 6^2 × (x + 5) $
D.$ \pi × 8^2 x = \pi × 6^2 × 5 $

答案： 4.A

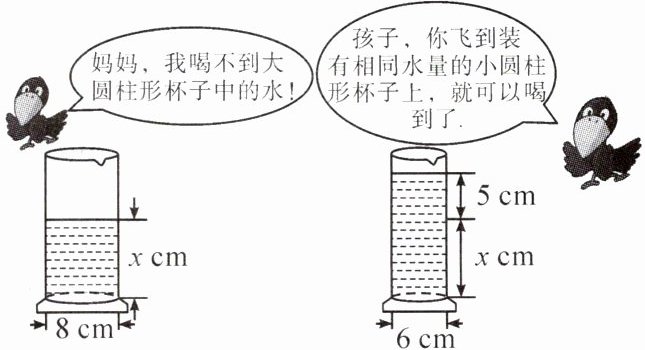
5. 如图，将一个正方形纸片先沿边剪去一个宽为 4 cm 的长方形纸条，再从剩下的长方形纸片上沿边剪去一个宽为 5 cm 的长方形纸条. 若两次剪下的长方形纸条的面积相等，则原正方形纸片的边长为20 cm.

答案： 5.20

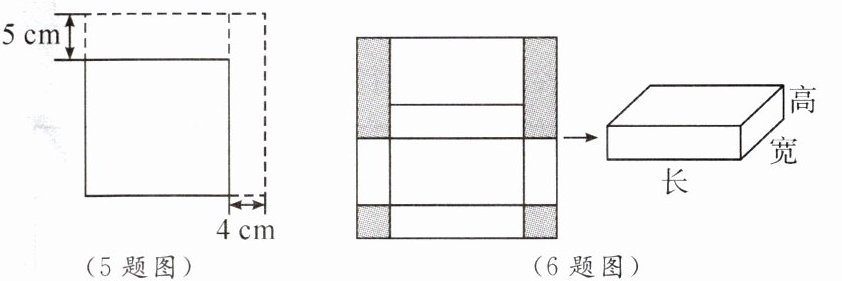
6. 边长为 30 cm 的正方形纸板如图所示，裁掉阴影部分后将其折叠成一个长方体盒子. 已知该长方体的宽是高的 2 倍，则它的体积是1000 cm³.

答案： 6.1000

7. 某足球比赛的计分规则为胜一场得 3 分，平一场得 1 分，负一场得 0 分. 一个队踢 14 场球负 5 场共得 19 分，这个队胜了几场？

答案： 7.解：设这个队胜了x场.由题意，得3x+(14-5-x)=19，解得x=5.答：这个队胜了5场.

8. 足球比赛的计分规则是：胜一场得 3 分，平一场得 1 分，负一场得 0 分. 一支足球队在整个赛季中共需比赛 14 场，现已比赛了 8 场，负了一场，得了 17 分.
(1) 前 8 场比赛中，这支球队共胜了多少场？
(2) 这支球队打满 14 场比赛，最高能得多少分？
(3) 通过对比赛情况的分析，这支球队打满 14 场比赛，得分不低于 29 分，就可以达到预期目标. 请分析一下，在后面的 6 场比赛中，这支球队至少要胜几场才能达到预期目标？

答案： 8.解：
(1)设前8场比赛中，这支球队共胜了x场，则3x+(8-x-1)=17，解得x=5.答：共胜了5场.
(2)17+(14-8)×3=35(分).答：最高能得35分.
(3)设至少要胜y场.由题意，得17+3y+(6-y)=29，解得y=3.答：这支球队至少要胜3场才能达到预期目标.