第11页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
1. 利用数轴比较有理数的大小:在数轴上表示的两个数,左边的数
2. 有理数比较大小的法则:
(1)正数
(2)两个负数,绝对值大的反而
小于
右边的数。2. 有理数比较大小的法则:
(1)正数
大于
0,0大于
负数,正数大于
负数;(2)两个负数,绝对值大的反而
小
。
答案:
1.小于 2.
(1)大于 大于 大于
(2)小
(1)大于 大于 大于
(2)小
例 1 解答下列问题。
(1)把下列各数用“<”连接起来:
$-5\frac{1}{2},$$\frac{2}{3},$0.7,-4.2,0,$\frac{3}{4}。$
(2)表示有理数 a,b 的点在数轴上的位置如图所示。把 a,-a,b,-b 按从小到大的顺序排列,正确的是(
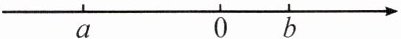
A. a < -a < -b < b
B. a < -b < -a < b
C. a < -b < b < -a
D. a < b < -b < -a
(3)最大的负整数是
(1)把下列各数用“<”连接起来:
$-5\frac{1}{2},$$\frac{2}{3},$0.7,-4.2,0,$\frac{3}{4}。$
(2)表示有理数 a,b 的点在数轴上的位置如图所示。把 a,-a,b,-b 按从小到大的顺序排列,正确的是(
C
)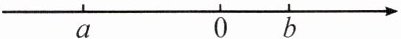
A. a < -a < -b < b
B. a < -b < -a < b
C. a < -b < b < -a
D. a < b < -b < -a
(3)最大的负整数是
-1
;绝对值最小的负整数是-1
;绝对值最小的有理数是0
。
答案:
(1)-5$\frac{1}{2}$ < -4.2 < 0 < $\frac{2}{3}$ < 0.7 < $\frac{3}{4}$。
(2)C
(3)-1 -1 0
(1)-5$\frac{1}{2}$ < -4.2 < 0 < $\frac{2}{3}$ < 0.7 < $\frac{3}{4}$。
(2)C
(3)-1 -1 0
例 2 先化简,再比较下列各组数的大小,用“<”连接:
(1)-|-14|与|-(-3)|;
$(2)+(-7\frac{1}{2})$与-|$-7\frac{7}{16}$|。
(1)-|-14|与|-(-3)|;
$(2)+(-7\frac{1}{2})$与-|$-7\frac{7}{16}$|。
答案:
(1)-|-14| < |-(-3)|;(2)+(-7$\frac{1}{2}$) < -|-7$\frac{7}{16}$|。
1. 表示数 a 的点在数轴上的位置如图所示。若数 b 满足 -a < b < a,则 b 的值可以是(
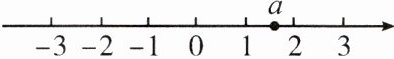
A.2
B.-1
C.-2
D.-3
B
)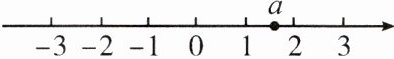
A.2
B.-1
C.-2
D.-3
答案:
1.B
2. (1)如图,请在数轴上表示下列各数:$-\frac{1}{2},$|-2.5|,-|+4|,-(-4)。
(2)将(1)中的各数用“<”连接起来。
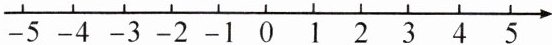
(2)将(1)中的各数用“<”连接起来。
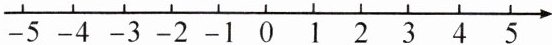
答案:
2.
(1)如图所示.

(2)-|+4| < -$\frac{1}{2}$ < |-2.5| < -(-4)。
2.
(1)如图所示.

(2)-|+4| < -$\frac{1}{2}$ < |-2.5| < -(-4)。
查看更多完整答案,请扫码查看


