第36页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
1. 乘方的定义:求 $ n $ 个
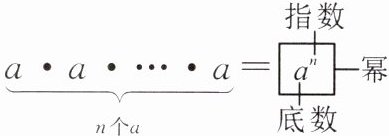
$\underbrace{a \cdot a \cdot \cdots \cdot a}_{n 个 a} = \begin{cases}a^n & 指数 \\幂 & \\底数 &\end{cases}$
2. 乘方的性质:
(1) 负数的奇次幂是
(2) 正数的任何正整数次幂都是
相同
乘数的 积
的运算,叫作乘方.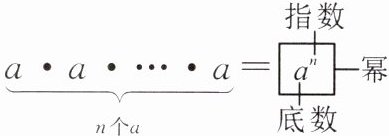
$\underbrace{a \cdot a \cdot \cdots \cdot a}_{n 个 a} = \begin{cases}a^n & 指数 \\幂 & \\底数 &\end{cases}$
2. 乘方的性质:
(1) 负数的奇次幂是
负数
,负数的偶次幂是 正数
;(2) 正数的任何正整数次幂都是
正数
,$ 0 $ 的任何正整数次幂都是 0
.
答案:
1.相同 积 2.
(1)负数 正数
(2)正数 0
(1)负数 正数
(2)正数 0
例题 解答下列问题.
(1) 比较下列每组数的异同,并计算出结果.
① $ 3^2 $ 与 $ 2^3 $;② $ (-3)^4 $ 与 $ -3^4 $;③ $ \left( \dfrac{2}{3} \right)^3 $ 与 $ \dfrac{2^3}{3} $.
(2) 填空:
① $ (-1)^{30} = $
② $ \left( -\dfrac{4}{5} \right)^3 = $
③ $ (-10)^3 = $
④ $ (-0.5)^3 = $
(3) 已知 $ (2a + 3)^{2026} + |b - 3| = 0 $,则 $ a^b $ 的值是
(1) 比较下列每组数的异同,并计算出结果.
① $ 3^2 $ 与 $ 2^3 $;② $ (-3)^4 $ 与 $ -3^4 $;③ $ \left( \dfrac{2}{3} \right)^3 $ 与 $ \dfrac{2^3}{3} $.
(2) 填空:
① $ (-1)^{30} = $
1
;② $ \left( -\dfrac{4}{5} \right)^3 = $
-\frac{64}{125}
;③ $ (-10)^3 = $
-1 000
;④ $ (-0.5)^3 = $
-0.125
.(3) 已知 $ (2a + 3)^{2026} + |b - 3| = 0 $,则 $ a^b $ 的值是
-\frac{27}{8}
.
答案:
(1)解:①3² 与2³的读法不同,底数和指数不同,运算结果不同,3²=9,2³=8.②(-3)⁴与-3⁴的读法不同,指数相同但底数不同,运算结果不同,(-3)⁴=81,-3⁴=-81.
$③(\frac{2}{3})³ $与$\frac{2^{3}}{3}$的读法不同,指数相同但底数不同,运算结果不同,$(\frac{2}{3})³=\frac{8}{27},$$\frac{2^{3}}{3}=\frac{8}{3}.$
$(2)①1 ②-\frac{64}{125} ③-1 000 ④-0.125$
$(3)-\frac{27}{8}$
(1)解:①3² 与2³的读法不同,底数和指数不同,运算结果不同,3²=9,2³=8.②(-3)⁴与-3⁴的读法不同,指数相同但底数不同,运算结果不同,(-3)⁴=81,-3⁴=-81.
$③(\frac{2}{3})³ $与$\frac{2^{3}}{3}$的读法不同,指数相同但底数不同,运算结果不同,$(\frac{2}{3})³=\frac{8}{27},$$\frac{2^{3}}{3}=\frac{8}{3}.$
$(2)①1 ②-\frac{64}{125} ③-1 000 ④-0.125$
$(3)-\frac{27}{8}$
1. 把 $ \left( -\dfrac{2}{3} \right) × \left( -\dfrac{2}{3} \right) × \left( -\dfrac{2}{3} \right) × \left( -\dfrac{2}{3} \right) $ 写成乘方的形式为
(\frac{-2}{3})⁴
.
答案:
$1.(\frac{-2}{3})⁴$
2. (1) 在 $ (-2)^4 $ 中,底数是 ____,指数是 ____,表示的意义为 ____;
(2) 在 $ -2^4 $ 中,底数是 ____,指数是 ____,表示的意义为 ____.
(2) 在 $ -2^4 $ 中,底数是 ____,指数是 ____,表示的意义为 ____.
答案:
2.
(1)-2 4 4个-2相乘的积
(2)2 4 4个2相乘的积的相反数
(1)-2 4 4个-2相乘的积
(2)2 4 4个2相乘的积的相反数
3. 数学文化《孙子算经》中记载有这样一个问题:今有出门望见九堤,堤有九木,木有九枝,枝有九巢……其大意是:某人走出门外,望见有 $ 9 $ 座堤坝,每座堤坝上有 $ 9 $ 棵树,每棵树上有 $ 9 $ 根树枝,每根树枝上有 $ 9 $ 个鸟巢……问题中的鸟巢共有
9⁴
个.
答案:
3.9⁴
4. 下列各组数互为相反数的是 (
A. $ 3^2 $ 与 $ -2^3 $
B. $ 3^2 $ 与 $ (-3)^2 $
C. $ 3^2 $ 与 $ -3^2 $
D. $ -2^3 $ 与 $ (-2)^3 $
C
)A. $ 3^2 $ 与 $ -2^3 $
B. $ 3^2 $ 与 $ (-3)^2 $
C. $ 3^2 $ 与 $ -3^2 $
D. $ -2^3 $ 与 $ (-2)^3 $
答案:
4.C
5. 填空:
(1) $ -(-6)^2 = $
(1) $ -(-6)^2 = $
-36
;(2) $ -\dfrac{2^3}{7} = $ -\frac{8}{7}
.
答案:
$5.(1)-36 (2)-\frac{8}{7}$
6. 已知 $ (a - 3)^2 $ 与 $ |4 - b| $ 互为相反数,则代数式 $ b^a - a^b $ 的值是
-17
.
答案:
6.-17
查看更多完整答案,请扫码查看


