《2025年超越训练七年级数学上册人教版四川专版》

12. 已知 $ (a - 2)^{2} + | b + 3 | = 0 $，$ | c | = (-2)^{2} $，求代数式 $ \frac{4ac - b^{2}}{4a} $的值.

答案： 12.解：因为$(a - 2)^{2} + \vert b + 3\vert = 0$，所以$a = 2$，$b = - 3$。因为$\vert c\vert = (-2)^{2} = 4$，所以$c = \pm 4$。①当$a = 2$，$b = - 3$，$c = 4$时，$\frac{4ac - b^{2}}{4a}=\frac{4× 2× 4 - (-3)^{2}}{4× 2}=\frac{23}{8}$；②当$a = 2$，$b = - 3$，$c = - 4$时，$\frac{4ac - b^{2}}{4a}=\frac{4× 2× (-4) - (-3)^{2}}{4× 2}=-\frac{41}{8}$。

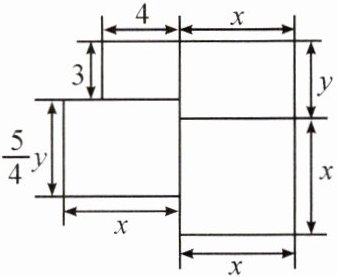
13. 一套住宅的建筑平面图如图所示（单位：m).
(1)求这套住宅的建筑面积（用含 $ x $，$ y $ 的代数式表示）.
(2)若该住宅的售价为 8800 元/$ m^{2} $，当 $ x = 6 $，$ y = 4 $ 时，求该住宅的总价为多少万元.

答案： 13.解：
(1)建筑面积为$(\frac{5}{4}xy + 12 + xy + x^{2})m^{2}$。
(2)当$x = 6$，$y = 4$时，$\frac{5}{4}xy + 12 + xy + x^{2}=\frac{5}{4} × 6 × 4 + 12 + 6 × 4 + 6^{2}=102$。$8800 × 102 = 897600(元)=89.76(万元)$。答：该住宅的总价为$89.76$万元。

14. 为了满足市场对口罩的需求，某工厂决定生产 $ A $，$ B $ 两种款式的口罩，每天两种口罩的生产量共 50000 个，两种口罩的成本和售价如下表所示.
设每天生产 $ A $ 种口罩 $ x $ 个.
(1)①每天生产 $ B $ 种口罩$(50000 - x)$个；
②用含 $ x $ 的代数式表示该工厂每天的生产成本.
(2)用含 $ x $ 的代数式表示该工厂每天获得的利润(利润 = 售价 - 成本).
(3)当 $ x = 20000 $ 时，求每天获得的利润.

答案： 14.解：
(1)①$(50000 - x)$。②由题意，得该工厂每天的生产成本为$[0.5x + 2.5(50000 - x)]$元。
(2)由题意，得该工厂每天获得的利润为$(1 - 0.5)x + (4 - 2.5)(50000 - x)=[0.5x + 1.5(50000 - x)]$元。
(3)当$x = 20000$时，$0.5x + 1.5(50000 - x)=0.5 × 20000 + 1.5 × (50000 - 20000)=55000$，即当$x = 20000$时，每天获得的利润为$55000$元。

15. 新学期，某中学计划添置 100 张课桌和 $ x $ 把椅子（$ x ＞ 100 $）.经调查发现，某家具厂的每张课桌定价 200 元，每把椅子定价 80 元.厂家在开展促销活动期间，面向客户提供了两种优惠方案.
方案一：每买一张课桌就赠送一把椅子；
方案二：课桌和椅子都按定价的 $ 80\% $付款.
(1)用含 $ x $ 的代数式分别表示两种方案各需付款多少元.
(2)当 $ x = 300 $ 时，选择哪种方案购买更省钱？

答案： 15.解：
(1)方案一需付款$200 × 100 + 80(x - 100)=[20000 + 80(x - 100)]$元。方案二需付款$200 × 80\% × 100 + 80 × 80\% x=(64x + 16000)$元。
(2)当$x = 300$时，方案一：$20000 + 80(x - 100)=20000 + 80 × (300 - 100)=36000$。方案二：$64x + 16000 = 64 × 300 + 16000 = 35200$。因为$36000 ＞ 35200$，所以选择方案二购买更省钱。