第29页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
7. 表示有理数 $a$,$b$,$c$,$d$ 的点在数轴上的位置如图所示,则 $abc$
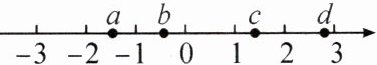
>
0,$bcd$<
0,$(-a)× b× c×(-d)$>
0.(填“$>$”或“$<$”)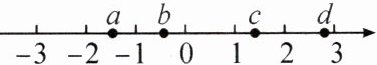
答案:
7.> < >
8. 若 $|a| = 5$,$|b| = 4$,且 $ab < 0$,则 $a - b$ 的最小值是
-9
.
答案:
8.-9
9. 已知 $a = -\frac{1}{2}$,$b = \frac{1}{3}$,$c = -3$,则 $(a - b)\cdot(a - c)\cdot(c - b)$ 的值是
\frac{125}{18}
.
答案:
$9.\frac{125}{18}$
10. 计算:
(1)$-2\frac{1}{3}×(-1.5)×(+\frac{3}{7})$;
(2)$1.25×(-1\frac{1}{7})×(-3.2)×(-\frac{7}{8})$;
(3)$4-(\frac{3}{8}+\frac{1}{6}-\frac{3}{4})×(-24)$;
(4)$3.59×(-\frac{4}{7})+2.41×(-\frac{4}{7})-6×(-\frac{4}{7})$.
(1)$-2\frac{1}{3}×(-1.5)×(+\frac{3}{7})$;
(2)$1.25×(-1\frac{1}{7})×(-3.2)×(-\frac{7}{8})$;
(3)$4-(\frac{3}{8}+\frac{1}{6}-\frac{3}{4})×(-24)$;
(4)$3.59×(-\frac{4}{7})+2.41×(-\frac{4}{7})-6×(-\frac{4}{7})$.
答案:
10.
(1)解:原式$= \frac{3}{2}. (2)$解:原式= -4.
(3)解:原式= -1.
(4)解:原式= 0.
(1)解:原式$= \frac{3}{2}. (2)$解:原式= -4.
(3)解:原式= -1.
(4)解:原式= 0.
11. 已知 $|a| = 10$,$|b| = 5$,且 $|ab| = -ab$,$c = -2$,求 $ac - bc$ 的值.
答案:
11.解:因为 |a| = 10,|b| = 5, 所以$ a = \pm 10,b = \pm 5. $因为 |ab| =
-ab, 所以$ ab \leq 0, $所以 a = 10,b = -5 或 a = -10,b = 5. 当 a =
10,b = -5 时,ac - bc = 10 × (-2) - (-5) × (-2) = -30; 当
a = -10,b = 5 时,ac - bc = (-10) × (-2) - 5 × (-2) = 30. 综
上所述,ac - bc 的值是 -30 或 30.
-ab, 所以$ ab \leq 0, $所以 a = 10,b = -5 或 a = -10,b = 5. 当 a =
10,b = -5 时,ac - bc = 10 × (-2) - (-5) × (-2) = -30; 当
a = -10,b = 5 时,ac - bc = (-10) × (-2) - 5 × (-2) = 30. 综
上所述,ac - bc 的值是 -30 或 30.
12. 已知 $abc > 0$,$a > c$,$ac < 0$,则下列结论正确的是(
A.$a < 0$,$b < 0$,$c > 0$
B.$a > 0$,$b > 0$,$c < 0$
C.$a > 0$,$b < 0$,$c < 0$
D.$a < 0$,$b > 0$,$c > 0$
C
)A.$a < 0$,$b < 0$,$c > 0$
B.$a > 0$,$b > 0$,$c < 0$
C.$a > 0$,$b < 0$,$c < 0$
D.$a < 0$,$b > 0$,$c > 0$
答案:
12.C
13. 表示有理数 $a$,$b$,$c$ 的点在数轴上的位置如图所示,则必有(
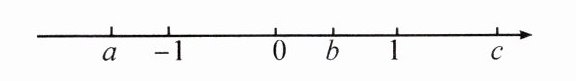
A.$abc > 0$
B.$ab - ac > 0$
C.$(a + b)c > 0$
D.$(a - c)b > 0$
B
)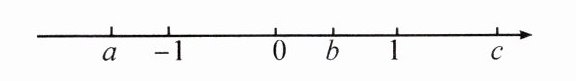
A.$abc > 0$
B.$ab - ac > 0$
C.$(a + b)c > 0$
D.$(a - c)b > 0$
答案:
13.B
14. 新定义定义一种新的运算“$\otimes$”,规则是 $a\otimes b = a×(b - 1)+(a + b)$.
(1)$(-2)\otimes(-3)$ 的值是
(2)求 $(3\otimes4)\otimes(-5)$ 的值.
(1)$(-2)\otimes(-3)$ 的值是
3
;(2)求 $(3\otimes4)\otimes(-5)$ 的值.
答案:
14.解:
(1)3.
(2)因为$ a \otimes b = a × (b - 1) + (a + b) = ab - a + a +$
b = ab + b = b × (a + 1), 所以$ 3 \otimes 4 = 4 × (3 + 1) = 16, $所以$ 16 \otimes$
(-5) = -5 × (16 + 1) = -85, 即$ (3 \otimes 4) \otimes (-5) = -85.$
(1)3.
(2)因为$ a \otimes b = a × (b - 1) + (a + b) = ab - a + a +$
b = ab + b = b × (a + 1), 所以$ 3 \otimes 4 = 4 × (3 + 1) = 16, $所以$ 16 \otimes$
(-5) = -5 × (16 + 1) = -85, 即$ (3 \otimes 4) \otimes (-5) = -85.$
查看更多完整答案,请扫码查看


