第85页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
1 如图,圆内接正六边形ABCDEF的周长为12cm,则该正六边形的内切圆半径为(
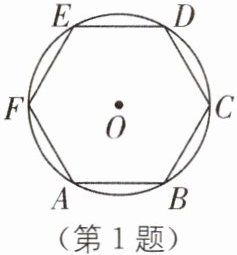
A.$\sqrt{3}$cm
B.2cm
C.$2\sqrt{3}$cm
D.$\sqrt{5}$cm
A
)。
A.$\sqrt{3}$cm
B.2cm
C.$2\sqrt{3}$cm
D.$\sqrt{5}$cm
答案:
A
2 数学文化 勒洛三角形 勒洛三角形是分别以等边三角形的顶点为圆心,以其边长为半径作圆弧,由三段圆弧组成的曲边三角形。如图,该勒洛三角形绕其中心O旋转一定角度α后能与自身重合,则该角度α可以为(
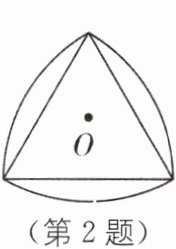
A.$30^{\circ}$
B.$60^{\circ}$
C.$120^{\circ}$
D.$150^{\circ}$
C
)。
A.$30^{\circ}$
B.$60^{\circ}$
C.$120^{\circ}$
D.$150^{\circ}$
答案:
【解析】:本题可根据旋转对称图形的性质来求解勒洛三角形绕中心$O$旋转后能与自身重合的角度。
旋转对称图形的定义为:把一个图形绕着一个定点旋转一个角度$\alpha$后,与初始图形重合,这种图形叫做旋转对称图形,这个定点叫做旋转对称中心,旋转的角度$\alpha$叫做这个旋转对称图形的一个旋转角。
对于勒洛三角形,它是分别以等边三角形的顶点为圆心,以其边长为半径作圆弧,由三段圆弧组成的曲边三角形。
等边三角形的内角均为$60^{\circ}$,且三条边相等,勒洛三角形绕其中心$O$旋转,由于它的对称性,绕中心$O$旋转的角度等于等边三角形内角的$2$倍时,能与自身重合。
等边三角形内角为$60^{\circ}$,那么$60^{\circ}×2 = 120^{\circ}$,即勒洛三角形绕其中心$O$旋转$120^{\circ}$后能与自身重合。
【答案】:C
旋转对称图形的定义为:把一个图形绕着一个定点旋转一个角度$\alpha$后,与初始图形重合,这种图形叫做旋转对称图形,这个定点叫做旋转对称中心,旋转的角度$\alpha$叫做这个旋转对称图形的一个旋转角。
对于勒洛三角形,它是分别以等边三角形的顶点为圆心,以其边长为半径作圆弧,由三段圆弧组成的曲边三角形。
等边三角形的内角均为$60^{\circ}$,且三条边相等,勒洛三角形绕其中心$O$旋转,由于它的对称性,绕中心$O$旋转的角度等于等边三角形内角的$2$倍时,能与自身重合。
等边三角形内角为$60^{\circ}$,那么$60^{\circ}×2 = 120^{\circ}$,即勒洛三角形绕其中心$O$旋转$120^{\circ}$后能与自身重合。
【答案】:C
3 (2025·南京秦淮区期末)如图,点O是边长为6的正六边形ABCDEF和边长为a的正方形MNPQ的中心,将正方形MNPQ绕点O旋转一周。若在旋转过程中,正方形MNPQ始终在正六边形ABCDEF的内部(即正方形边上的所有点都在正六边形内),则a的取值范围是______。
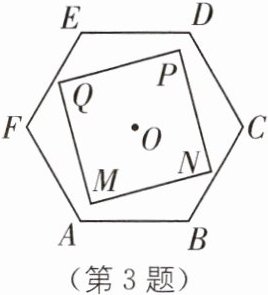

答案:
0<a<3$\sqrt{6}$ [解析]如图,当正方形MNPQ的一个顶点Q 在EF的中点时,正方形MNPQ的边长最大,

连接OE、OF、OQ、OP,则OQ⊥EF,
∵六边形ABCDEF是正六边形,中心为O,
∴∠EOF=$\frac{360^{\circ}}{6}$=60°,OE=OF,
∴△EOF是正三角形,
∴OE=OF=EF=6,QE=QF=3,
在Rt△EOQ中,EQ=3,OE=6,
∴OQ= $\sqrt{OE^{2}-EQ^{2}}$=3$\sqrt{3}$
在Rt△POQ中,PQ=$\sqrt{2}$OQ=3$\sqrt{6}$,
即正方形MNPQ的边长最大为3$\sqrt{6}$
∴a的取值范围是0<a<3$\sqrt{6}$
0<a<3$\sqrt{6}$ [解析]如图,当正方形MNPQ的一个顶点Q 在EF的中点时,正方形MNPQ的边长最大,

连接OE、OF、OQ、OP,则OQ⊥EF,
∵六边形ABCDEF是正六边形,中心为O,
∴∠EOF=$\frac{360^{\circ}}{6}$=60°,OE=OF,
∴△EOF是正三角形,
∴OE=OF=EF=6,QE=QF=3,
在Rt△EOQ中,EQ=3,OE=6,
∴OQ= $\sqrt{OE^{2}-EQ^{2}}$=3$\sqrt{3}$
在Rt△POQ中,PQ=$\sqrt{2}$OQ=3$\sqrt{6}$,
即正方形MNPQ的边长最大为3$\sqrt{6}$
∴a的取值范围是0<a<3$\sqrt{6}$
4 如图,A、B、C、D为⊙O上的点,且直线AB与CD夹角为$45^{\circ}$。若$\overset{\frown}{AB}$、$\overset{\frown}{AC}$、$\overset{\frown}{CD}$的长分别为π、π和3π,则⊙O的半径是( )。
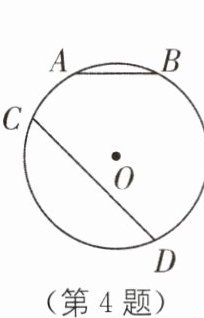
A.4
B.4.5
C.5
D.5.5

A.4
B.4.5
C.5
D.5.5
答案:
A [解析]
∵$\overset{\frown}{AB}$、$\overset{\frown}{AC}$、$\overset{\frown}{CD}$的长分别为π、π和3π,
∴$\overset{\frown}{BC}$的长为2π,$\overset{\frown}{AD}$的长为4π.
如图,延长BA,交DC的延长线于
点E.由题意,知∠E=45°,
连接BD,设弧长为π的弧所对的
 圆周角为α,⊙O的半径为R,则
圆周角为α,⊙O的半径为R,则
∠BDC=2α,∠ABD=4α.
∵∠BDC+∠ABD+∠E=180°,
∠E=45°,
∴2α+4α+45°=180°,
∴α=$\frac{45^{\circ}}{2}$,
∴弧长为π的弧所对的圆心角为$\frac{45^{\circ}}{2}$×2=45°,
∴$\frac{45\pi\cdot R}{180}$=π,
∴R=4.故选A.
A [解析]
∵$\overset{\frown}{AB}$、$\overset{\frown}{AC}$、$\overset{\frown}{CD}$的长分别为π、π和3π,
∴$\overset{\frown}{BC}$的长为2π,$\overset{\frown}{AD}$的长为4π.
如图,延长BA,交DC的延长线于
点E.由题意,知∠E=45°,
连接BD,设弧长为π的弧所对的
 圆周角为α,⊙O的半径为R,则
圆周角为α,⊙O的半径为R,则∠BDC=2α,∠ABD=4α.
∵∠BDC+∠ABD+∠E=180°,
∠E=45°,
∴2α+4α+45°=180°,
∴α=$\frac{45^{\circ}}{2}$,
∴弧长为π的弧所对的圆心角为$\frac{45^{\circ}}{2}$×2=45°,
∴$\frac{45\pi\cdot R}{180}$=π,
∴R=4.故选A.
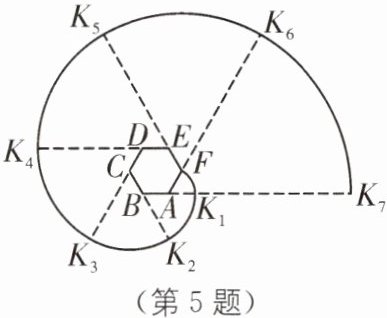
5 如图,六边形ABCDEF是边长为1的正六边形,曲线$FK_{1}K_{2}K_{3}K_{4}K_{5}K_{6}K_{7}……$叫做“正六边形的渐开线”,其中$\overset{\frown}{FK_{1}}$、$\overset{\frown}{K_{1}K_{2}}$、$\overset{\frown}{K_{2}K_{3}}$、$\overset{\frown}{K_{3}K_{4}}$、$\overset{\frown}{K_{4}K_{5}}$、$\overset{\frown}{K_{5}K_{6}}……$的圆心依次按点A、B、C、D、E、F循环,一电子宠物从点F出发,沿着“渐开线”爬至点$K_{7}$的路径长为(
A.$\frac{7}{3}\pi$
B.$7\pi$
C.$9\pi$
D.$\frac{28}{3}\pi$
D
)。
A.$\frac{7}{3}\pi$
B.$7\pi$
C.$9\pi$
D.$\frac{28}{3}\pi$
答案:
D [解析]正六边形的一个外角的度数为$\frac{360^{\circ}}{6}$=60°,
∴每条弧所对圆心角的度数为60°.
设$\overset{\frown}{FK_{1}}$、$\overset{\frown}{K_{1}K_{2}}$、$\overset{\frown}{K_{2}K_{3}}$、$\overset{\frown}{K_{3}K_{4}}$、$\overset{\frown}{K_{4}K_{5}}$、$\overset{\frown}{K_{5}K_{6}}$……的弧长分别为$l_{1}$、$l_{2}$、$l_{3}$、$l_{4}$、$l_{5}$、$l_{6}$……,
由题图可知$l_{1}=\frac{60}{180}\pi×1=\frac{\pi}{3}$,$l_{2}=\frac{60}{180}\pi×2=\frac{2\pi}{3}$,$l_{3}=\frac{60}{180}\pi×3=\pi$,$l_{4}=\frac{60}{180}\pi×4=\frac{4\pi}{3}$……,由此规律可知,$l_{7}=\frac{60}{180}\pi×7=\frac{7\pi}{3}$
∴一电子宠物从点F出发,沿着“渐开线”爬至点$K_{7}$的路径长为$l_{1}+l_{2}+l_{3}+l_{4}+l_{5}+l_{6}+l_{7}=\frac{(1 + 2 + 3+\cdots+7)}{3}\pi=\frac{28\pi}{3}$.故选D.
∴每条弧所对圆心角的度数为60°.
设$\overset{\frown}{FK_{1}}$、$\overset{\frown}{K_{1}K_{2}}$、$\overset{\frown}{K_{2}K_{3}}$、$\overset{\frown}{K_{3}K_{4}}$、$\overset{\frown}{K_{4}K_{5}}$、$\overset{\frown}{K_{5}K_{6}}$……的弧长分别为$l_{1}$、$l_{2}$、$l_{3}$、$l_{4}$、$l_{5}$、$l_{6}$……,
由题图可知$l_{1}=\frac{60}{180}\pi×1=\frac{\pi}{3}$,$l_{2}=\frac{60}{180}\pi×2=\frac{2\pi}{3}$,$l_{3}=\frac{60}{180}\pi×3=\pi$,$l_{4}=\frac{60}{180}\pi×4=\frac{4\pi}{3}$……,由此规律可知,$l_{7}=\frac{60}{180}\pi×7=\frac{7\pi}{3}$
∴一电子宠物从点F出发,沿着“渐开线”爬至点$K_{7}$的路径长为$l_{1}+l_{2}+l_{3}+l_{4}+l_{5}+l_{6}+l_{7}=\frac{(1 + 2 + 3+\cdots+7)}{3}\pi=\frac{28\pi}{3}$.故选D.
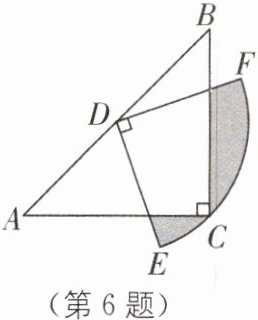
6 新情境 面积问题 如图,在$\triangle ABC$中,$CA= CB= 4$,$\angle ACB= 90^{\circ}$,以AB的中点D为圆心,作圆心角为$90^{\circ}$的扇形DEF,点C恰好在弧EF上,则图中阴影部分面积为______。

答案:
2π−4 [解析]如图,连接CD,设AC、
DE交于点N,BC、DF交于点M.
 在△ABC中,CA=CB=4,
在△ABC中,CA=CB=4,
∠ACB=90°,
∴AB=4$\sqrt{2}$
∵以AB的中点D为圆心,作圆心角
为90°的扇形DEF,点C恰好在$\overset{\frown}{EF}$上,
∴CD=2$\sqrt{2}$、∠B=∠DCB=∠ACD=45°,CD=BD.
∵∠ADC=∠BDC=∠EDF=90°,
∴∠CDN+∠CDF=90°,∠CDF+∠BDM=90°.
∴∠BDM=∠CDN.
在△BDM和△CDN中,$\begin{cases}\angle B = \angle DCN\\BD = CD\\\angle BDM = \angle CDN\end{cases}$
∴△BDM≌△CDN(ASA).
∴△CDN与△CDM的面积之和等于△CDM与△BDM 的面积之和,
∴四边形DNCM的面积等于△CDB的面积,
∴阴影部分的面积为$S_{扇形DEF}-S_{\triangle CDB}=\frac{90\pi×(2\sqrt{2})^{2}}{360}-\frac{2\sqrt{2}×2\sqrt{2}}{2}=2\pi - 4$.
2π−4 [解析]如图,连接CD,设AC、
DE交于点N,BC、DF交于点M.
 在△ABC中,CA=CB=4,
在△ABC中,CA=CB=4,∠ACB=90°,
∴AB=4$\sqrt{2}$
∵以AB的中点D为圆心,作圆心角
为90°的扇形DEF,点C恰好在$\overset{\frown}{EF}$上,
∴CD=2$\sqrt{2}$、∠B=∠DCB=∠ACD=45°,CD=BD.
∵∠ADC=∠BDC=∠EDF=90°,
∴∠CDN+∠CDF=90°,∠CDF+∠BDM=90°.
∴∠BDM=∠CDN.
在△BDM和△CDN中,$\begin{cases}\angle B = \angle DCN\\BD = CD\\\angle BDM = \angle CDN\end{cases}$
∴△BDM≌△CDN(ASA).
∴△CDN与△CDM的面积之和等于△CDM与△BDM 的面积之和,
∴四边形DNCM的面积等于△CDB的面积,
∴阴影部分的面积为$S_{扇形DEF}-S_{\triangle CDB}=\frac{90\pi×(2\sqrt{2})^{2}}{360}-\frac{2\sqrt{2}×2\sqrt{2}}{2}=2\pi - 4$.
7 (2024·南京秦淮区期末)圆锥的底面半径为3cm,母线长为5cm,则圆锥的表面积为
24π
$cm^{2}$。
答案:
24π
8 (2024·句容期末)已知扇形AOB的半径为6cm,圆心角的度数为$120^{\circ}$,若将此扇形围成一个圆锥的侧面,则围成的圆锥的底面圆的半径为
2
cm。
答案:
【解析】:
本题主要考查了圆锥的计算以及扇形的弧长公式。题目给出了扇形AOB的半径和圆心角的度数,以及这个扇形将被围成一个圆锥的侧面。我们需要求出这个圆锥的底面圆的半径。
首先,我们需要知道扇形的弧长公式:弧长 = 圆心角的度数/360° × 2π × 半径。
根据题目,扇形AOB的半径为6cm,圆心角的度数为120°,所以扇形的弧长为:
弧长 = $\frac{120}{360} × 2\pi × 6 = 4\pi$ (cm)。
这个弧长实际上就是圆锥底面的周长,因为我们将扇形围成了一个圆锥的侧面。
圆锥底面的周长公式为:周长 = 2πr,其中r是圆锥底面的半径。
由此,我们可以得到方程:4π = 2πr。
解这个方程,我们可以得到:r = 2 (cm)。
所以,围成的圆锥的底面圆的半径为2cm。
【答案】:
2
本题主要考查了圆锥的计算以及扇形的弧长公式。题目给出了扇形AOB的半径和圆心角的度数,以及这个扇形将被围成一个圆锥的侧面。我们需要求出这个圆锥的底面圆的半径。
首先,我们需要知道扇形的弧长公式:弧长 = 圆心角的度数/360° × 2π × 半径。
根据题目,扇形AOB的半径为6cm,圆心角的度数为120°,所以扇形的弧长为:
弧长 = $\frac{120}{360} × 2\pi × 6 = 4\pi$ (cm)。
这个弧长实际上就是圆锥底面的周长,因为我们将扇形围成了一个圆锥的侧面。
圆锥底面的周长公式为:周长 = 2πr,其中r是圆锥底面的半径。
由此,我们可以得到方程:4π = 2πr。
解这个方程,我们可以得到:r = 2 (cm)。
所以,围成的圆锥的底面圆的半径为2cm。
【答案】:
2
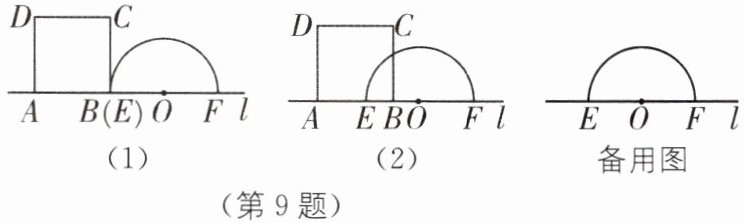
9 如图(1),矩形ABCD与以EF为直径的半圆O在直线l的上方,线段AB与点E、F都在直线l上,且$AB= 7$,$EF= 10$,$BC>5$。点B以1个单位/秒的速度从点E处出发,沿射线EF方向运动,矩形ABCD随之运动,运动时间为t秒。
(1)如图(2),当$t= 2.5$时,求半圆O在矩形ABCD内的弧的长度;
(2)在点B运动的过程中,当AD、BC都与半圆O相交时,设这两个交点为G、H。连接OG、OH,若$\angle GOH$为直角,求此时t的值。
(1)如图(2),当$t= 2.5$时,求半圆O在矩形ABCD内的弧的长度;
(2)在点B运动的过程中,当AD、BC都与半圆O相交时,设这两个交点为G、H。连接OG、OH,若$\angle GOH$为直角,求此时t的值。

答案:
(1)如图
(1),设BC与⊙O交于点M,
当t = 2.5时,BE = 2.5.
∵EF = 10,
∴OE=$\frac{1}{2}$EF = 5,
∴OB = 2.5,
∴EB = OB.
在矩形ABCD中,
∵∠ABC = 90°,
∴ME = MO.
又MO = EO,
∴ME = EO = MO,
∴△MOE是等边三角形,
∴∠EOM = 60°,
∴$l_{\overset{\frown}{ME}}=\frac{60\pi×5}{180}=\frac{5\pi}{3}$.
故半圆O在矩形ABCD内的弧的长度为$\frac{5\pi}{3}$.

(2)如图
(2),连接GO、HO,
∵∠GOH = 90°,
∴∠AOG + ∠BOH = 90°.
∵∠AGO + ∠AOG = 90°,
∴∠AGO = ∠BOH.
在△AGO和△BOH中,$\begin{cases}\angle AGO = \angle BOH\\\angle GAO = \angle OBH\\OG = HO\end{cases}$
∴△AGO≌△BOH(AAS),
∴AG = OB = EB - OE = t - 5.
∵AB = 7,
∴AE = EB - AB = t - 7.
∴AO = OE - AE = 5 - (t - 7)=12 - t.
在Rt△AGO中,$AG^{2}+AO^{2}=OG^{2}$,
∴$(t - 5)^{2}+(12 - t)^{2}=5^{2}$,
解得$t_{1}=8$,$t_{2}=9$,故t的值为8或9.
(1)如图
(1),设BC与⊙O交于点M,
当t = 2.5时,BE = 2.5.
∵EF = 10,
∴OE=$\frac{1}{2}$EF = 5,
∴OB = 2.5,
∴EB = OB.
在矩形ABCD中,
∵∠ABC = 90°,
∴ME = MO.
又MO = EO,
∴ME = EO = MO,
∴△MOE是等边三角形,
∴∠EOM = 60°,
∴$l_{\overset{\frown}{ME}}=\frac{60\pi×5}{180}=\frac{5\pi}{3}$.
故半圆O在矩形ABCD内的弧的长度为$\frac{5\pi}{3}$.

(2)如图
(2),连接GO、HO,
∵∠GOH = 90°,
∴∠AOG + ∠BOH = 90°.
∵∠AGO + ∠AOG = 90°,
∴∠AGO = ∠BOH.
在△AGO和△BOH中,$\begin{cases}\angle AGO = \angle BOH\\\angle GAO = \angle OBH\\OG = HO\end{cases}$
∴△AGO≌△BOH(AAS),
∴AG = OB = EB - OE = t - 5.
∵AB = 7,
∴AE = EB - AB = t - 7.
∴AO = OE - AE = 5 - (t - 7)=12 - t.
在Rt△AGO中,$AG^{2}+AO^{2}=OG^{2}$,
∴$(t - 5)^{2}+(12 - t)^{2}=5^{2}$,
解得$t_{1}=8$,$t_{2}=9$,故t的值为8或9.
查看更多完整答案,请扫码查看


