第79页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
1 (教材P77思考与探索·拓展)下列说法:①各边都相等的多边形是正多边形;②各边都相等的圆的内接多边形是正多边形;③各角都相等的圆的内接多边形是正多边形;④各角都相等的多边形是正多边形。其中正确的有(
A.1个
B.2个
C.3个
D.4个
A
)。A.1个
B.2个
C.3个
D.4个
答案:
A [解析]根据正多边形的定义,各边都相等,各内角都相等的多边形叫做正多边形,故①③④不正确;圆的内接多边形,只要各边都相等,可以证明各角也都相等,所以②正确。故选A。
2 如图,正五边形ABCDE内接于⊙O,连接OC、OD,则∠BAE-∠COD= (
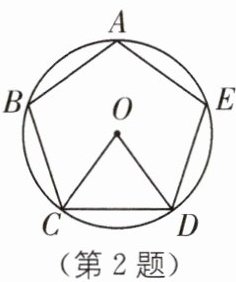
A.60°
B.54°
C.48°
D.36°
D
)。
A.60°
B.54°
C.48°
D.36°
答案:
D [解析]
∵五边形ABCDE是正五边形,
∴∠BAE=(5 - 2)×180°/5 = 108°,∠COD = 360°/5 = 72°,
∴∠BAE - ∠COD = 108° - 72° = 36°。故选D。
∵五边形ABCDE是正五边形,
∴∠BAE=(5 - 2)×180°/5 = 108°,∠COD = 360°/5 = 72°,
∴∠BAE - ∠COD = 108° - 72° = 36°。故选D。
3 (2024·南京玄武区期末)如图,已知正五边形ABCDE,经过C、D两点的⊙O与AB、AE分别相切于点M、N,连接CM、CN,则∠MCN= ______°。
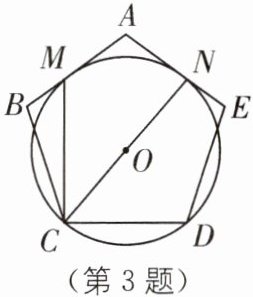

答案:
36 [解析]如图,连接OM,
∵⊙O与AB、AE分别相切于点M、N,
∴∠OMA = ∠ONA = 90°。
∵多边形ABCDE是五边形,
∴∠A = (5 - 2)×180÷5 = 108°,
∴∠MON = 180° - ∠A = 72°。
∵$\overset{\frown}{MN}$ = $\overset{\frown}{MN}$,
∴∠MCN = $\frac{1}{2}$∠NOM = $\frac{1}{2}$×72° = 36°。
36 [解析]如图,连接OM,
∵⊙O与AB、AE分别相切于点M、N,
∴∠OMA = ∠ONA = 90°。
∵多边形ABCDE是五边形,
∴∠A = (5 - 2)×180÷5 = 108°,
∴∠MON = 180° - ∠A = 72°。
∵$\overset{\frown}{MN}$ = $\overset{\frown}{MN}$,
∴∠MCN = $\frac{1}{2}$∠NOM = $\frac{1}{2}$×72° = 36°。

4 (教材P78例题·变式)一个正多边形的中心角为36°,则它的边数是
10
。
答案:
10 [解析]由题意,得360°÷36° = 10,
∴它的边数是10。
∴它的边数是10。
5 (教材P79尝试与交流·拓展)关于正多边形的对称性,下列说法正确的是(
A.正多边形都是中心对称图形
B.正多边形都是轴对称图形
C.没有既是中心对称图形又是轴对称图形的正多边形
D.正多形的所有对称轴都经过它的中心和两条边的中点
B
)。A.正多边形都是中心对称图形
B.正多边形都是轴对称图形
C.没有既是中心对称图形又是轴对称图形的正多边形
D.正多形的所有对称轴都经过它的中心和两条边的中点
答案:
B [解析]根据正多边形中,偶数边形既是中心对称图形,又是轴对称图形,奇数边形是轴对称图形,但不是中心对称图形,奇数边形的对称轴经过它的中心、一个角的顶点和一条边的中点,可以判断A、C、D错误。故选B。
6 正八边形有
8
条对称轴,它不仅是轴
对称图形,还是中心
对称图形。
答案:
8 轴 中心
7 新情境 构建模型 在冬奥会开幕式和闭幕式中,一片“雪花”的故事展现了“世界大同、天下一家”的主题,让世界观众感受了中国人的浪漫。如图,将“雪花”图案(边长为4的正六边形ABCDEF)放在平面直角坐标系中,若AB与x轴垂直,顶点A的坐标为(2,-3),则顶点C的坐标为( )。
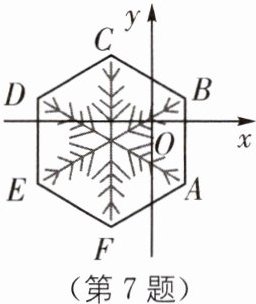
A.(2-2√3,3)
B.(0,1+2√3)
C.(2-√3,3)
D.(2-2√3,2+√3)

A.(2-2√3,3)
B.(0,1+2√3)
C.(2-√3,3)
D.(2-2√3,2+√3)
答案:
A [解析]如图,连接BD交CF于点M。由题易知点B(2,1)。在Rt△BCM中,BC = 4,∠BCM = $\frac{1}{2}$×120° = 60°,
∴CM = $\frac{1}{2}$BC = 2,BM = $\frac{\sqrt{3}}{2}$BC = 2$\sqrt{3}$,
∴点C的横坐标为-(2$\sqrt{3}$ - 2) = 2 - 2$\sqrt{3}$,纵坐标为1 + 2 = 3,
∴点C的坐标为(2 - 2$\sqrt{3}$,3)。故选A。
A [解析]如图,连接BD交CF于点M。由题易知点B(2,1)。在Rt△BCM中,BC = 4,∠BCM = $\frac{1}{2}$×120° = 60°,
∴CM = $\frac{1}{2}$BC = 2,BM = $\frac{\sqrt{3}}{2}$BC = 2$\sqrt{3}$,
∴点C的横坐标为-(2$\sqrt{3}$ - 2) = 2 - 2$\sqrt{3}$,纵坐标为1 + 2 = 3,
∴点C的坐标为(2 - 2$\sqrt{3}$,3)。故选A。

8 (2025·南京玄武区期末)如图,在正五边形ABCDE中,连接CE,以E为圆心,EA长为半径画弧,与CE交于点F,连接AF,则∠AFE的度数是
54
°。
答案:
54 [解析]在正五边形ABCDE中,
∵∠AED = ∠CDE = (5 - 2)×180°/5 = 108°,DE = CD,
∴∠DCE = ∠CED = $\frac{1}{2}$×(180° - 108°) = 36°,
∴∠AEF = 108° - 36° = 72°。
∵AE = EF,
∴∠EAF = ∠AFE = $\frac{1}{2}$×(180° - 72°) = 54°。
∵∠AED = ∠CDE = (5 - 2)×180°/5 = 108°,DE = CD,
∴∠DCE = ∠CED = $\frac{1}{2}$×(180° - 108°) = 36°,
∴∠AEF = 108° - 36° = 72°。
∵AE = EF,
∴∠EAF = ∠AFE = $\frac{1}{2}$×(180° - 72°) = 54°。
9 (教材P80操作与思考·拓展)(1)利用尺规作图,八等分图中的圆,从而画一个圆的内接正八边形(不写作法,保留作图痕迹);
(2)若(1)中圆的半径为2,求所画正八边形的面积。
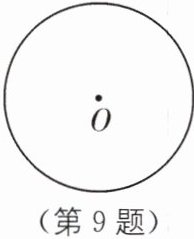
(2)若(1)中圆的半径为2,求所画正八边形的面积。

答案:
(1)如图所示正八边形AECGBFDH即为所求,作法提示:①画两条互相垂直的直径AB、CD;②连接AC、BC,并作AC和BC的垂直平分线,分别交圆O于E、F、G、H;③顺次连接A、E、C、G、B、F、D、H各点,得如图所示正八边形即为所求。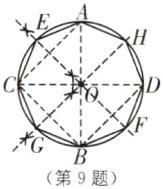
(2)如图,连接BD,由画图,得∠BOD = 90°,△BOD是等腰直角三角形,
∴BD = $\sqrt{2}$OB = 2$\sqrt{2}$,此时BD与OF垂直,
∴S四边形OBFD = $\frac{1}{2}$×BD×OF = $\frac{1}{2}$×2×2$\sqrt{2}$ = 2$\sqrt{2}$,
∴正八边形面积为2$\sqrt{2}$×4 = 8$\sqrt{2}$。
(1)如图所示正八边形AECGBFDH即为所求,作法提示:①画两条互相垂直的直径AB、CD;②连接AC、BC,并作AC和BC的垂直平分线,分别交圆O于E、F、G、H;③顺次连接A、E、C、G、B、F、D、H各点,得如图所示正八边形即为所求。

(2)如图,连接BD,由画图,得∠BOD = 90°,△BOD是等腰直角三角形,
∴BD = $\sqrt{2}$OB = 2$\sqrt{2}$,此时BD与OF垂直,
∴S四边形OBFD = $\frac{1}{2}$×BD×OF = $\frac{1}{2}$×2×2$\sqrt{2}$ = 2$\sqrt{2}$,
∴正八边形面积为2$\sqrt{2}$×4 = 8$\sqrt{2}$。
查看更多完整答案,请扫码查看


