《2025年课时训练九年级数学上册苏科版江苏人民出版社》

1 教材P24问题1·改编 用一根长22cm的铁丝围成面积是$30cm^2$的矩形.假设矩形的一边长是xcm,则可列出方程(B).
A.x(22-x)= 30
B.x(11-x)= 30
C.x(22-2x)= 30
D.2x(22-x)= 30

答案： B

2 教材P30习题T5·改编 (2024·昭通永善二模)如图,在一块长为36米,宽为25米的矩形空地上修建三条宽均为x米的笔直小道,其余部分(即图中阴影部分)改造为草坪进行绿化,若草坪的面积为840平方米,求x的值.根据题意,下列方程正确的是(D).
A.36×25-36x-25x= 840
B.36x+25x= 840

$C.(36-x)(25-x)+x^2= 840$
D.(36-x)(25-x)= 840

答案： D

3 教材P25练习T1·变式 传统文化《中秋帖》《中秋帖》是晋朝书法家王献之的作品,若在一幅长为65cm、宽为30cm的《中秋帖》矩形书法作品的四周镶上相同宽度的金色纸边,制成一幅矩形挂图,设金色纸边的宽为xcm,如果要使整个挂图的面积是$2450cm^2,$那么x满足的方程是(65+2x)(30+2x)=2450.

答案： (65+2x)(30+2x)=2450

4 教材P29习题T4·变式 如图,把小圆形场地的半径增加5m得到大圆形场地,场地面积增加了一倍,则小圆形场地的半径(r)为(5+5$\sqrt{2}$)m.

答案： (5+5$\sqrt{2}$)m

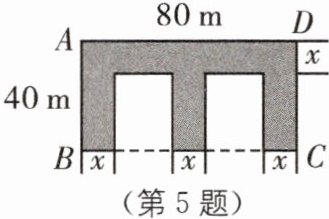
5 教材P30习题T5·变式 某学校有一长方形空地ABCD,长80m,宽40m,计划在这块空地上划出如图所示宽度相等的E形区域作为花圃,已知花圃区域的面积为$1700m^2,$求该花圃的宽度x(单位:m).

答案： 由题意,得80×40-(80-3x)(40-x)=1700，整理,得3$x^2$-200x+1700=0,解得$x_1$=10,$x_2$=$\frac{170}{3}$(舍去).故该花圃的宽度x为10 m.

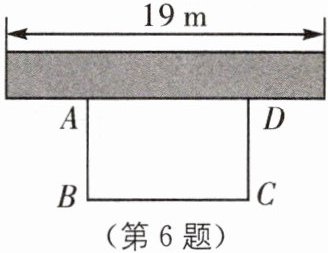
6(2024·扬州广陵区期末)如图,学校为美化环境,在靠墙的一侧设计了一块矩形花圃ABCD,其中,墙长19m,花圃三边外围用篱笆围起,共用篱笆30m.
(1)若花圃的面积为$100m^2,$求花圃一边AB的长.
(2)花圃的面积能达到$120m^2$吗?说明理由.

答案：
(1)设AB的长为x m,由题意,得x(30-2x)=100,解得$x_1$=5,$x_2$=10.
∵30-2x≤19,
∴x=10.故AB的长为10 m.
(2)花圃的面积不能达到120$m^2$.理由如下：设AB的长为y m,由题意,得y(30-2y)=120,化简,得$y^2$-15y+60=0.
∵$\Delta$=(-15)$^2$-4×60=-15＜0,
∴方程无解,
∴花圃的面积不能达到120$m^2$.