《2025年课时训练九年级数学上册苏科版江苏人民出版社》

1(2025·徐州新沂期中)如图,AB是$\odot O$的弦,点P为优弧APB上的一点,$∠APB的平分线交\odot O$于点Q,$AB= 6,∠APB= 60^{\circ }$,则在点P运动的过程中,PQ长的最大值为( ).

A.$2\sqrt {3}$
B.$4\sqrt {3}$
C.6
D.$3+2\sqrt {3}$

答案：
B [解析]如图,连接 AQ,由题意，当 PQ 为⊙O 的直径时，PQ 的长最大。
∵PQ 平分∠APB，
∴∠APQ = ∠BPQ = $\frac{1}{2}$∠APB = 30°，
∴$\widehat{AQ}$ = $\widehat{BQ}$。
∵PQ 为⊙O 的直径，
∴$\widehat{AP}$ = $\widehat{BP}$，∠PAQ = 90°，
∴AP = PB。又∠APB = 60°，
∴△PAB 是等边三角形，
∴AP = AB = 6。在 Rt△APQ 中，
∵∠APQ = 30°，
∴PQ = 2AQ，
∴AP² = PQ² - AQ² = $\frac{3}{4}$PQ²，
∴PQ² = $\frac{4}{3}$×6² = 48，则 PQ = 4$\sqrt{3}$，即在点 P 运动的过程中，PQ 长的最大值为 4$\sqrt{3}$。故选 B。

变式1.1 (2025·徐州睢宁期中)如图,AB是$\odot O$的弦,C是优弧AmB上一动点,连接AC、BC,点D、E分别是AB、BC的中点,连接DE.若$AB= 2\sqrt {3},∠ACB= 60^{\circ }$,则DE的最大值为____2.

答案： 2 [解析]
∵点 D、E 分别是 AB、BC 的中点，
∴DE = $\frac{1}{2}$AC，
∴当 AC 取得最大值时，DE 就取得最大值，且当 AC 是直径时最大。
∵AC 是直径时∠B = 90°，又∠ACB = 60°，AB = 2$\sqrt{3}$，
∴由勾股定理易得 AC = 4，
∴DE = $\frac{1}{2}$AC = 2，
∴DE 的最大值为 2。

变式1.2 如图,AB、BC是以O为圆心,半径为4的圆的两条弦,$∠B= 60^{\circ }$,且点O在$∠B$内,则$AC= $____,若点D是劣弧AC上的一个动点,点M、N、P分别是AD、CD、BC的中点.则$PN+MN$的长度的最大值为____.

答案：
4$\sqrt{3}$ 2$\sqrt{3}$ + 4 [解析]如图，连接 OC、OA、BD，作 OH⊥AC 于 H。
∵∠ABC = 60°，
∴∠AOC = 2∠ABC = 120°。
∵OA = OC，OH⊥AC，
∴∠COH = ∠AOH = 60°，CH = AH，
∴∠OCH = 30°，
∴OH = $\frac{1}{2}$OC = 2，
∴CH = $\sqrt{OC² - OH²}$ = 2$\sqrt{3}$，
∴AC = 4$\sqrt{3}$。
∵M、N 分别是 AD、CD 的中点，
∴MN = $\frac{1}{2}$AC = 2$\sqrt{3}$。
∵P、N 分别是 BC、CD 的中点，
∴PN = $\frac{1}{2}$BD，
∴当 BD 是直径时，PN 的值最大，最大值为 4，
∴PN + MN 的最大值为 4 + 2$\sqrt{3}$。

2 如图,等腰直角三角形ABC的一个锐角顶点A是$\odot O$上的一个动点,$∠ACB= 90^{\circ }$,腰AC与斜边AB分别交$\odot O$于
点E、D,分别过点D、E作$\odot O$的切线交于点F,且点F恰好是腰BC上的点,连接OC、OD、OE,若$\odot O$的半径为4,则OC的最大值为( ).

A.$2\sqrt {5}+2$
B.$4\sqrt {2}+2$
C.6
D.8

答案：
A [解析]
∵在等腰直角三角形 ABC 中，∠ACB = 90°，
∴∠A = ∠B = 45°，
∴∠DOE = 2∠A = 90°。
∵分别过点 D、E 作⊙O 的切线，
∴OD⊥DF，OE⊥EF，
∴四边形 ODFE 是矩形。
∵OD = OE = 4，
∴四边形 ODFE 是正方形，
∴EF = 4。
∵点 F 恰好是腰 BC 上的点，
∴∠ECF = 90°，
∴点 C 在以 EF 为直径的半圆上运动，
∴设 EF 的中点为 G，则 EG = FG = CG = $\frac{1}{2}$EF = 2，且当 OC 经过半圆圆心 G 时，OC 的值最大，此时，在 Rt△OEG 中，OG = $\sqrt{OE² + EG²}$ = $\sqrt{4² + 2²}$ = 2$\sqrt{5}$，
∴OC = OG + CG = 2$\sqrt{5}$ + 2。故选 A。

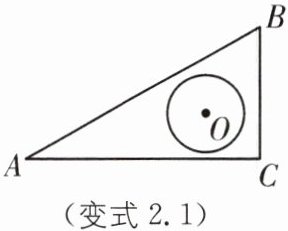
变式2.1 (2024·河北秦皇岛十五中期末)如图,在$Rt△ABC$中,$∠C= 90^{\circ },AC= 6,BC= 2\sqrt {3}$,半径为1的$\odot O在Rt△ABC$内平移($\odot O$可以与该三角形的边相切),则点A到$\odot O$上的点的距离的最大值为( ).

A.$\sqrt {7}+1$
B.$2\sqrt {7}+1$
C.$2\sqrt {7}-1$
D.$3\sqrt {7}-1$

答案：
B [解析]设直线 AO 交⊙O 于点 M（M 在 O 点右边），则点 A 到⊙O 上的点的距离的最大值为 AM 的长度，当⊙O 与 AB、BC 相切时，AM 最长。设切点分别为 D、F，连接 OB、OD、OF，如图，
∵∠C = 90°，AC = 6，BC = 2$\sqrt{3}$，AB = $\sqrt{AC² + BC²}$ = 4$\sqrt{3}$，
∴∠BAC = 30°，∠ABC = 60°。
∵⊙O 与 AB、BC 相切，
∴∠OBD = $\frac{1}{2}$∠ABC = 30°。
∵⊙O 的半径为 1，
∴OD = OM = 1，
∴OB = 2，
∴BD = $\sqrt{OB² - OD²}$ = $\sqrt{3}$，
∴AD = AB - DB = 3$\sqrt{3}$，
∴OA = $\sqrt{AD² + OD²}$ = $\sqrt{(3\sqrt{3})^{2} + 1^{2}}$ = 2$\sqrt{7}$，
∴AM = OA + OM = 2$\sqrt{7}$ + 1，
∴点 A 到⊙O 上的点的距离的最大值为 2$\sqrt{7}$ + 1。故选 B。

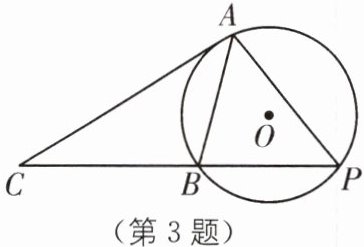
3(2025·湖北武汉新洲区月考)如图,$\odot O$的半径为4,弦AB的长为$4\sqrt {3}$,点P为优弧AB上一动点,$AC⊥AP$交直线PB于点C,则$△ABC$的面积的最大值是( ).

A.$12\sqrt {3}+12$
B.$6\sqrt {3}+12$
C.$12\sqrt {3}+24$
D.$6\sqrt {3}+24$

答案：
C [解析]如图，连接 OA、OB，过点 O 作 OD⊥AB于点 D。
∵OD⊥AB，
∴AD = DB = 2$\sqrt{3}$，∠AOD = ∠BOD，
∴OD = $\sqrt{OA² - AD²}$ = 2，
∴∠OAD = 30°，
∴∠AOD = ∠BOD = 60°，
∴∠AOB = 120°，
∴∠P = $\frac{1}{2}$∠AOB = 60°。
∵AP⊥AC，
∴∠CAP = 90°，
∴∠C = 30°，
∴点 C 在以 O'为圆心，OA 为半径的圆上运动，当点 C 在 AB 的垂直平分线上时，△ABC 的面积最大。
∵∠AO'B = 2∠AC'B = 60°，O'A = O'B，
∴△AO'B 是等边三角形，
∴O'A = O'C' = AB = 4$\sqrt{3}$，O'D = $\sqrt{O'A² - AD²}$ = 6，
∴C'D = 4$\sqrt{3}$ + 6，
∴△ABC 面积的最大值为 $\frac{1}{2}$AB·C'D = $\frac{1}{2}$×4$\sqrt{3}$×(4$\sqrt{3}$ + 6) = 24 + 12$\sqrt{3}$。故选 C。

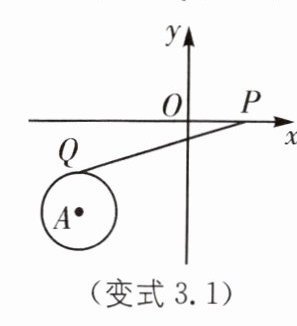
变式3.1 如图,点A的坐标为$(-3,-2),\odot A$的半径为1,P为x轴上一动点,PQ切$\odot A$于点Q,则当PQ取最小值时,点P的坐标为( ).


A.$(-4,0)$
B.$(-2,0)$
C.$(-4,0)或(-2,0)$
D.$(-3,0)$

答案：
D [解析]连接 AQ、AP。根据切线的性质定理，得 AQ⊥PQ。要使 PQ 最小，只需 AP 最小，根据垂线段最短，可知当 AP⊥x 轴时，AP 最短，
∴点 P 的坐标是(-3,0)。故选 D。