《2025年课时训练九年级数学上册苏科版江苏人民出版社》

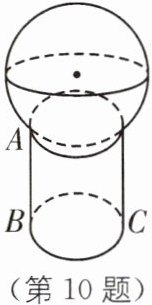
10 (2024·无锡惠山区期末)如图,将一个球放在空心的透明圆柱形玻璃瓶上,测得瓶高$AB= 20cm$,底面直径$BC= 16cm$,球的最高点到地面的距离为36cm,则球的半径为____cm.(玻璃瓶厚度忽略不计)

答案：
10 [解析]如图，设球的半径为 R cm.由题意可知，AB=CD=EF=20 cm，BC=AD=16 cm，GF=36 cm，则 AE=DE= $\frac{1}{2}$AD=8 cm，OE=(36-20-R)cm.在 Rt△AOE 中，由勾股定理，得 OA²=OE²+AE²，即 R²=(16-R)²+8²，解得 R=10，即球的半径为 10 cm.
　　　　　　　　　　　　　　　　　　　

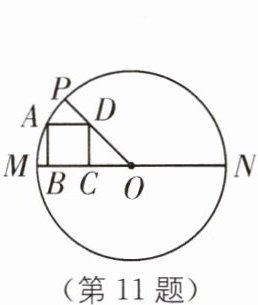
11 原创素养题 几何直观 如图,在$\odot O$中,直径$MN= 10$,正方形ABCD的四个顶点分别在半径OM、OP以及$\odot O$上,并且$∠POM= 45^{\circ }$,则AB的长为____.

答案：
$\sqrt{5}$ [解析]如图，连接 AO.
∵四边形 ABCD 是正方形，
∴∠DCO=90°.
∵∠POM=45°，
∴∠CDO=45°，
∴CD=CO，
　　　　　　　　　　　　　　　　
∴BO=BC+CO=BC+CD，
∴BO=2AB.
∵MN=10，
∴AO=5.在 Rt△ABO 中，AB²+BO²=AO²，即 AB²+(2AB)²=5²，
∴AB= $\sqrt{5}$.

12 中考新考法 新定义问题 定义:到一个三角形三个顶点的距离相等的点叫做该三角形的外心.
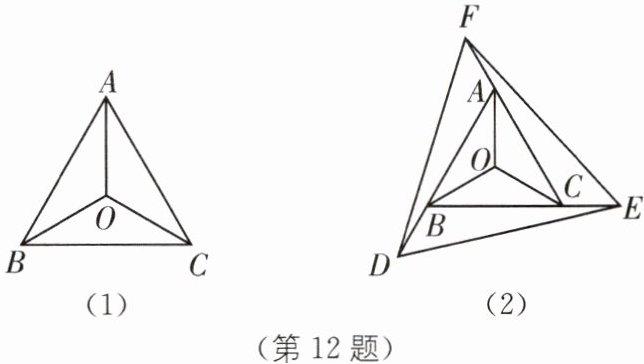
(1)如图(1),$△ABC$是等边三角形,点O是$△ABC$的外心,求证:$∠ABO= 30^{\circ };$
(2)如图(2),$△ABC$是等边三角形,分别延长等边三角形ABC的边AB、BC、CA到点D、E、F,使$BD= CE= AF$,连接DE、EF、DF.若点O为$△ABC$的外心,求证:点O也是$△DEF$的外心.

答案：

(1)
∵△ABC 是等边三角形，
∴∠ABC=60°，AB=AC=BC.
∵点 O 是△ABC 的外心，
∴OA=OB=OC.
　　在△AOB 与△COB 中，$\begin{cases} AB=CB, \\ OB=OB, \\ OA=OC, \end{cases}$
∴△AOB≌△COB(SSS)，
∴∠ABO=∠OBC.
∵∠ABO+∠OBC=∠ABC=60°，
∴∠ABO=30°.
(2)如图，连接 OF、OD、OE.
　　由
(1)，得∠ABO=30°.
∵点 O 为△ABC 的外心，
∴OA=OB，
∴∠OAB=∠ABO=30°，
∴∠OAC=60°-30°=30°，
∴180°-∠OAC=180°-∠ABO，
∴∠FAO=∠DBO.
　　在△FAO 与△DBO 中，$\begin{cases} AF=BD, \\ ∠FAO=∠DBO, \\ AO=BO, \end{cases}$
∴△FAO≌△DBO(SAS)，
∴OF=OD.
　　同理，OF=OE.
∴OF=OE=OD，
∴点 O 也是△DEF 的外心.
　　　　　　　　　　　　　　　

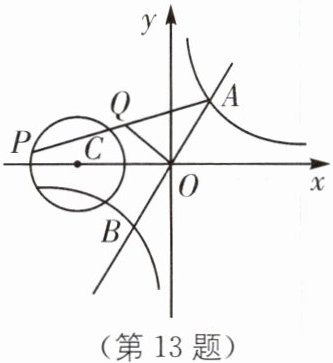
13 如图,正比例函数$y= 2x与反比例函数y= \frac {32}{25x}$的图像交于A、B两点,点P在以$C(-2,0)$为圆心,1为半径的$\odot C$上运动,点Q是AP的中点,求OQ长的最大值.

答案：
联立正比例函数 y=2x 与反比例函数 y= $\frac{32}{25x}$，得$\begin{cases} y=2x, \\ y=\frac{32}{25x}, \end{cases}$解得$\begin{cases} x=\frac{4}{5}, \\ y=\frac{8}{5} \end{cases}$或$\begin{cases} x=-\frac{4}{5}, \\ y=-\frac{8}{5} \end{cases}$.
∴点 A 的坐标为($\frac{4}{5}$,$\frac{8}{5}$)，点 B 的坐标为(-$\frac{4}{5}$,-$\frac{8}{5}$).如图，连接 BP，连接 BC 并延长交圆 C 于点 D.由反比例函数图像的对称性可知点 O 为 AB 的中点，
∵点 Q 为 AP 的中点，
∴OQ= $\frac{1}{2}$PB，
∴所求 OQ 长的最大值，在 PB 长为最大值时取到.当点 P 运动到点 D 时，BP 取得最大值，即为 BD 的长.过点 B 作 BE⊥x 轴于点 E，则 OE= $\frac{4}{5}$，BE= $\frac{8}{5}$.
∵点 C 的坐标为(-2,0)，
∴OC=2，CE=CO-OE= $\frac{6}{5}$.由勾股定理，得 BC= $\sqrt{BE^2+CE^2}=2$，
∴BD=BC+CD=3，
∴OQ 长的最大值为 $\frac{3}{2}$.
　　　　　　　　　　　　　　　

14 一题多问 圆心到弦的距离叫做该弦的弦心距.
[数学理解]如图(1),在$\odot O$中,AB是弦,$OP⊥AB$,垂足为P,则OP的长是弦AB的弦心距.
(1)若$\odot O$的半径为5,弦AB的弦心距为3,则AB的长为____.
(2)若$\odot O$的半径确定,下列关于AB的长随着OP的长的变化而变化的结论:
①AB的长随着OP的长的增大而增大;
②AB的长随着OP的长的增大而减小;
③AB的长与OP的长无关.
其中所有正确结论的序号是____.
[问题解决](3)若弦心距等于该弦长的一半,则这条弦所对的圆心角的度数为____$^{\circ }$.
(4)已知如图(2)给定的线段EF和$\odot O$,点Q是$\odot O$内一定点.过点Q作弦AB,满足$AB= EF$,请问这样的弦可以作____条.

答案：

(1)8 [解析]如图
(1)，连接 OA.
∵OP⊥AB，
∴AP=BP= $\frac{1}{2}$AB.
　　　　　　　　　　　　　　　　　
在 Rt△OAP 中，由勾股定理，得 AP= $\sqrt{OA^2-OP^2}=4$，
∴AB=2AP=8.
(2)② [解析]设⊙O 的半径为 r(r＞0)，OP=x(x＞0).由
(1)知，AB=2AP，AP= $\sqrt{OA^2-OP^2}$，
∴AB²=(2AP)²=4AP²=4(OA²-OP²)=4(r²-x²)=-4x²+4r².
∵⊙O 的半径确定，即 r 的值为定值，
∴x 的值越大，AB²的值越小，AB 的长度越小，即 AB 的长度随 OP 的长的增大而减小.故正确结论的序号是②.
(3)90 [解析]如图
(2)，连接 OA、OB.
∵弦心距等于该弦长的一半，
∴OP=AP，
　　　　　　　　　　　　　　　　　
∴∠AOP=45°，
∴∠AOB=2∠AOP=90°.
(4)2 [解析]经过测量 EF 的长度小于⊙O 的直径，故根据圆的轴对称性质可知，这样的弦可以作 2 条.