《2025年课时训练九年级数学上册苏科版江苏人民出版社》

6 $\odot O$的半径为13cm,弦$AB// CD$,$AB= 10cm$,$CD= 24cm$,则AB与CD之间的距离是____。

答案：
17cm或7cm　[解析]如图,作OE⊥AB于点E,OF⊥CD于点F,连接OA、OC.
由题意,得OA=OC=13cm,
AE=$\frac{1}{2}$AB=5cm,
CF=$\frac{1}{2}$CD=12cm.
∵AB//CD,
∴E、O、F三点共线.
在Rt△COF中,OF=$\sqrt{OC^2-CF^2}$=5(cm),
在Rt△AOE中,OE=$\sqrt{OA^2-AE^2}$=12(cm).
当弦AB与CD在圆心O的异侧时，AB与CD的距离为OE+OF=12+5=17(cm);
当弦A'B'与CD在圆心O的同侧时,A'B'与CD的距离为OE−OF=12−5=7(cm).
故AB与CD的距离是17cm或7cm.
　　　　　　　　　　　　　　　

7 如图,I是$\triangle ABC$的内心,$∠A= 50^{\circ}$,则$∠BIC= $115°。

答案： 115°　[解析]根据三角形内心是角平分线的交点可知，BI、CI分别平分∠ABC、∠ACB,
∴∠BIC=180°−$\frac{1}{2}$(∠ABC+∠ACB)=180°−$\frac{1}{2}$(180°−50°)=115°.

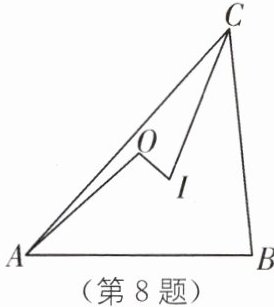
8 如图,点O、I分别是锐角三角形ABC的外心、内心,若$∠CAB= 8∠OAC= 48^{\circ}$,则$∠AOI-∠CIO= $____$^{\circ}$。

答案：
30　[解析]如图,连接OC,连接BO并延长，交AC于点H.
∵∠CAB=8∠OAC=48°,
∴∠OAC=6°,
∵点O为△ABC的外心，
∴OA=OC,
　　　　　　　　　　　　　　　
∴∠OCA=∠OAC=6°,
∴∠AOC=180°−6°−6°=168°,
∴∠ABC=$\frac{1}{2}$∠AOC=84°.
∵∠ACB+∠CAB+∠ABC=180°,
∴∠ACB=180°−48°−84°=48°,
∴BA=BC.
∴BO垂直平分AC,
∴OB平分∠ABC.
又点I是△ABC的内心，
∴△ABC的内心I在OB上.
∵BH⊥AC,
∴∠AOI=∠AHO+∠OAH=90°+6°=96°.
∵I为△ABC的内心,
∴CI平分∠ACB,
∴∠BCI=$\frac{1}{2}$∠ACB=24°.
同理可得∠CBI=$\frac{1}{2}$∠ABC=42°,
∴∠CIO=∠CBI+∠BCI=42°+24°=66°,
∴∠AOI−∠CIO=96°−66°=30°.
归纳总结　本题考查了三角形的内切圆与内心:三角形的内心到三角形三边的距离相等;三角形的内心与三角形顶点的连线平分这个内角，也考查了三角形的外心和圆周角定理.

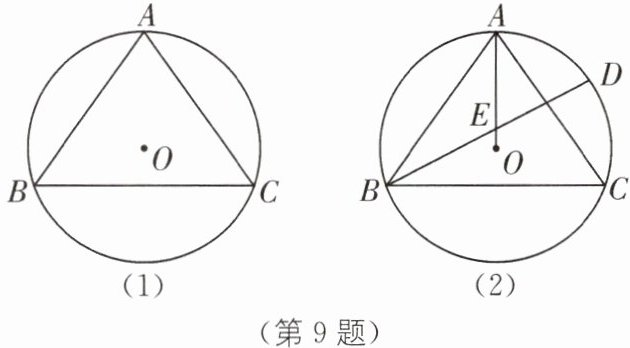
9 在$\triangle ABC$中,$AB= AC= 5$,$BC= 6$,$\odot O是\triangle ABC$的外接圆。
(1)如图(1),求$\odot O$的半径；
(2)如图(2),$∠ABC$的平分线交半径OA于点E,交$\odot O$于点D,求OE的长。

答案：

(1)如图
(1),过点A作AH⊥BC于点H,连接OB.
∵AB=AC,BC=6,
∴BH=CH=$\frac{1}{2}$BC=3,
即AH垂直平分BC,
∴点O在AH上.
在Rt△ABH中,AH=$\sqrt{5^2-3^2}$=4.
设⊙O的半径为r,则OB=r,OH=AH−OA=4−r.在Rt△OBH中,由勾股定理,得3²+(4−r)²=r²,
解得r=$\frac{25}{8}$,即⊙O的半径为$\frac{25}{8}$.
　　　
(2)如图
(2),过点E作EF⊥AB于点F,延长AO交BC 于点H,则OH⊥BC.
∵BD平分∠ABC,
∴EH=EF.
∵S△ABE=$\frac{1}{2}$BH·AE=$\frac{1}{2}$AB·EF,
∴$\frac{EF}{AE}=\frac{BH}{AB}=\frac{3}{5}$,
∴EH=EF=$\frac{3}{8}$AH=$\frac{3}{8}$×4=$\frac{3}{2}$.
由
(1),得半径为$\frac{25}{8}$,
∴OH=AH−OA=4−$\frac{25}{8}$=$\frac{7}{8}$,
∴OE=EH−OH=$\frac{3}{2}$−$\frac{7}{8}$=$\frac{5}{8}$.

10 如图,AB是$\odot O$的直径,点D在AB的延长线上,DC切$\odot O$于点C,若$∠A= 20^{\circ}$,则$∠D$等于(C)。

A.$20^{\circ}$
B.$30^{\circ}$
C.$50^{\circ}$
D.$40^{\circ}$

答案： C

11 如图,在$Rt\triangle ABC$中,$∠ACB= 90^{\circ}$,$AC= 3$,$BC= 4$,以C为圆心,r为半径的圆与边AB有公共点,则r的取值范围为(D)。

A.$r≥\frac{12}{5}$
B.$r= 3或r= 4$
C.$\frac{12}{5}≤r≤3$
D.$\frac{12}{5}≤r≤4$

答案： D　[解析]过点C作CD⊥AB于点D.
∵∠ACB=90°,AC=3,BC=4,
∴AB=5.
∵S△ABC=$\frac{1}{2}$AB·CD=$\frac{1}{2}$AC·BC,
∴CD=$\frac{AC·BC}{AB}=\frac{12}{5}$,
即圆心C到AB的距离d=$\frac{12}{5}$.
∵AC＜BC,
∴以C为圆心,$\frac{12}{5}$或4为半径所作的圆与斜边AB只有一个公共点，
∴若⊙C与斜边AB有公共点，则r的取值范围是$\frac{12}{5}$≤r≤4.故选D.
思路引导　本题考查了直线与圆的位置关系、勾股定理以及直角三角形的性质，审题时要注意圆与边AB有公共点和圆与直线AB有公共点的区别.

12 如图,扇形OAB是一个圆锥的侧面展开图,若小正方形方格的边长为1,则这个圆锥的底面半径为$\frac{5}{4}$。

答案： $\frac{5}{4}$　[解析]根据勾股定理，得OA=OB=$\sqrt{3^2+4^2}$=5,AB=$\sqrt{1^2+7^2}=5\sqrt{2}$.
∵OA²+OB²=AB²,
∴△AOB为直角三角形,
∴∠AOB=90°.
设这个圆锥的底面半径为r，
根据题意,得2πr=$\frac{90×π×5}{180}$,解得r=$\frac{5}{4}$.
故这个圆锥的底面半径为$\frac{5}{4}$.
名师点评　需用勾股定理逆定理证明△AOB为直角三角形，或结合方格，也可以用三角形全等证明∠AOB=90°.

13 如图,$\odot O是\triangle ABC$的外接圆,点O在$\triangle ABC$内,若$∠BCO= 40^{\circ}$,则$∠A= $50$^{\circ}$。

答案： 50　[解析]连接OB.
∵OB=OC,
∴∠OBC=∠BCO=40°,
∴∠BOC=100°,
∴∠A=$\frac{1}{2}$∠BOC=50°.

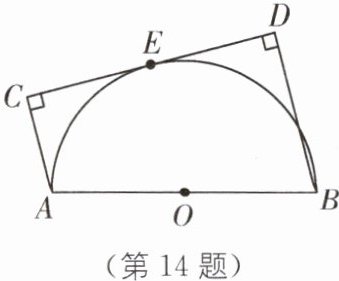
14 如图,以AB为直径画半圆O,CD与半圆O相切,切点为E,过A、B分别作CD的垂线,垂足分别为C、D,若$AC= 2$,$CD= 6$,则BD的长为____。

答案：
$\frac{9}{2}$　[解析]如图,连接OE、AE、BE,过点A作AF⊥BD 于点F,则∠AFB=∠AFD=90°,易证点F在半圆上,四边形AFDC为矩形,易证OE⊥AF于点G,G为AF的中点,E为CD的中点.
由勾股定理,得AC²+CE²=AE²,DE²+BD²=BE²,AE²+BE²=AB²,AF²+BF²=AB²,
∴AC²+CE²+DE²+BD²=AF²+BF²,
设BD=x,易得DF=AC=2,CE=DE=3,AF=CD=6,BF=x−2,
∴2²+3²+3²+x²=6²+(x−2)²,解得x=$\frac{9}{2}$,故BD=$\frac{9}{2}$.