第101页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
1 教材 P113 尝试与交流·拓展 (2024·宿迁宿豫区期末)为了考察某种小麦的长势,从中抽取了5株麦苗,测得苗高(单位:cm)为:10、16、9、17、19,则这组数据的极差是(
A.8
B.9
C.10
D.11
C
).A.8
B.9
C.10
D.11
答案:
C
2 分类讨论思想 若一组数据-1、0、2、4、x的极差为6,则x的值是(
A.-2
B.2或-5
C.5
D.5或-2
D
).A.-2
B.2或-5
C.5
D.5或-2
答案:
D
3 教材 P116 练习 T2·变式 数据1、2、3、4、5的方差是(
A.$\sqrt{2}$
B.2
C.3
D.5
B
).A.$\sqrt{2}$
B.2
C.3
D.5
答案:
B [解析]
∵$\overline{x}=\frac{1+2+3+4+5}{5}=3$,
∴$s^{2}=\frac{1}{5}×[(1-3)^{2}+(2-3)^{2}+(3-3)^{2}+(4-3)^{2}+(5-3)^{2}]=2$.故选B.
∵$\overline{x}=\frac{1+2+3+4+5}{5}=3$,
∴$s^{2}=\frac{1}{5}×[(1-3)^{2}+(2-3)^{2}+(3-3)^{2}+(4-3)^{2}+(5-3)^{2}]=2$.故选B.
对于一组数据$x_{1}$、$x_{2}$、$x_{3}$、…、$x_{n}$,可用如下算式计算方差:$s^{2}= \frac{1}{n}[(x_{1}-5)^{2}+(x_{2}-5)^{2}+(x_{3}-5)^{2}+…+(x_{n}-5)^{2}]$,其中“5”是这组数据的(
A.最小值
B.平均数
C.中位数
D.众数
B
).A.最小值
B.平均数
C.中位数
D.众数
答案:
解:方差的计算公式为$s^{2}=\frac{1}{n}[(x_{1}-\overline{x})^{2}+(x_{2}-\overline{x})^{2}+\cdots+(x_{n}-\overline{x})^{2}]$,其中$\overline{x}$是这组数据的平均数。题目中给出的方差算式为$s^{2}=\frac{1}{n}[(x_{1}-5)^{2}+(x_{2}-5)^{2}+\cdots+(x_{n}-5)^{2}]$,与方差公式对比可知,“5”是这组数据的平均数。
答案:B
答案:B
5 (2025·无锡期末)某射击爱好者的8次射击成绩(单位:环)依次为7、9、10、8、9、8、10、10,则下列结论正确的是(
A.众数是9环
B.中位数是9环
C.平均数是8环
D.方差是1.2环$^2$
B
).A.众数是9环
B.中位数是9环
C.平均数是8环
D.方差是1.2环$^2$
答案:
B
6 某中学为了选拔一名运动员参加市运会100米短跑比赛,有甲、乙两名运动员备选,他们最近测试的10次百米跑平均时间都是12.83秒,他们的方差分别是$s_{甲}^{2}= 1.3$秒^2,$s_{乙}^{2}= 1.7$秒^2,如果要选择一名成绩优秀且稳定的人去参赛,应派
甲
去.
答案:
甲 [解析]
∵$s_{甲}^{2}=1.3$秒$^{2}$,$s_{乙}^{2}=1.7$秒$^{2}$,
∴$s_{甲}^{2}<s_{乙}^{2}$.又甲、乙的10次百米跑平均时间相同,
∴选择一名成绩优秀且稳定的人去参赛,应派甲去.
∵$s_{甲}^{2}=1.3$秒$^{2}$,$s_{乙}^{2}=1.7$秒$^{2}$,
∴$s_{甲}^{2}<s_{乙}^{2}$.又甲、乙的10次百米跑平均时间相同,
∴选择一名成绩优秀且稳定的人去参赛,应派甲去.
7 甲、乙两名队员参加射击训练,成绩分别被制成如图的两个统计图:
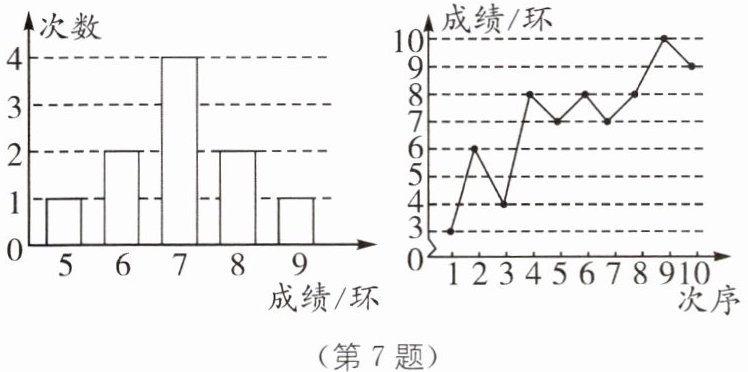
根据以上信息,整理分析数据如下:
| |平均成绩/环|中位数/环|众数/环|方差|
|甲|a|7|7|1.2|
|乙|7|b|8|c|
(1)写出表格中a、b、c的值.
(2)分别运用表中的四个统计量,简要分析这两名队员的射击训练成绩.若选派其中一名参赛,你认为应选哪名队员?

根据以上信息,整理分析数据如下:
| |平均成绩/环|中位数/环|众数/环|方差|
|甲|a|7|7|1.2|
|乙|7|b|8|c|
(1)写出表格中a、b、c的值.
(2)分别运用表中的四个统计量,简要分析这两名队员的射击训练成绩.若选派其中一名参赛,你认为应选哪名队员?
答案:
(1)$a=\frac{5×1+6×2+7×4+8×2+9×1}{1+2+4+2+1}=7$.
∵乙射击的成绩从小到大重新排列为3、4、6、7、7、8、8、8、9、10,
∴乙射击成绩的中位数$b=\frac{7+8}{2}=7.5$.乙的方差$c=\frac{1}{10}×[(3-7)^{2}+(4-7)^{2}+(6-7)^{2}+2×(7-7)^{2}+3×(8-7)^{2}+(9-7)^{2}+(10-7)^{2}]=\frac{1}{10}×(16+9+1+3+4+9)=4.2$.
(2)从平均成绩看,甲、乙二人的成绩相等,均为7环;从中位数看,甲射中7环以上的次数小于乙;从众数看,甲射中7环的次数最多,而乙射中8环的次数最多;从方差看,甲的成绩比乙的成绩稳定.综合以上各因素,若选派一名学生参加比赛的话,可选择乙参赛,因为乙获得高分的可能更大.
(1)$a=\frac{5×1+6×2+7×4+8×2+9×1}{1+2+4+2+1}=7$.
∵乙射击的成绩从小到大重新排列为3、4、6、7、7、8、8、8、9、10,
∴乙射击成绩的中位数$b=\frac{7+8}{2}=7.5$.乙的方差$c=\frac{1}{10}×[(3-7)^{2}+(4-7)^{2}+(6-7)^{2}+2×(7-7)^{2}+3×(8-7)^{2}+(9-7)^{2}+(10-7)^{2}]=\frac{1}{10}×(16+9+1+3+4+9)=4.2$.
(2)从平均成绩看,甲、乙二人的成绩相等,均为7环;从中位数看,甲射中7环以上的次数小于乙;从众数看,甲射中7环的次数最多,而乙射中8环的次数最多;从方差看,甲的成绩比乙的成绩稳定.综合以上各因素,若选派一名学生参加比赛的话,可选择乙参赛,因为乙获得高分的可能更大.
若一组数据1、3、5、7、x的方差比另一组数据11、13、15、17、19的方差小,则x不可以是(
A.10
B.8
C.6
D.4
A
).A.10
B.8
C.6
D.4
答案:
A [解析]数据11、13、15、17、19中,相邻两个数相差为2,一组数据1、3、5、7、x前4个数据也是相差2,当x=9或x=-1时,两组数据方差相等,故若数据1、3、5、7、x的方差比另一组数据11、13、15、17、19的方差小,则x的值不可能是10.故选A.
日常生活中,某些技能的训练,新手通常表现不太稳定.以下是小李和小林进行射击训练10次射击完成之后的成绩统计,请根据图中信息估计谁可能是新手(
A.小李
B.小林
C.都可能是新手
D.无法判定
A
).A.小李
B.小林
C.都可能是新手
D.无法判定
答案:
A
查看更多完整答案,请扫码查看


