《2025年课时训练九年级数学上册苏科版江苏人民出版社》

(1)若该公司当月售出3辆汽车,则每辆汽车的进价为26.8万元.
(2)如果汽车的售价为28万元/辆,该公司计划当月盈利12万元,那么需要售出多少辆汽车?(盈利= 销售利润+返利)
设需要售出x辆汽车,由题意知,每辆汽车的销售利润为$28-[27-0.1(x-1)]=(0.1x+0.9)$万元.当$0\leqslant x\leqslant 10$时,根据题意,得$x(0.1x+0.9)+0.5x=12$,整理,得$x^{2}+14x-120=0$,解得$x_{1}=-20$(不合题意,舍去),$x_{2}=6$.当$x＞10$时,根据题意,得$x(0.1x+0.9)+x=12$,整理,得$x^{2}+19x-120=0$,解得$x_{1}=-24$(不合题意,舍去),$x_{2}=5$.因为$5＜10$,所以$x=5$不合题意,需舍去.故需要售出6辆汽车.

答案：
(1)26.8
(2)设需要售出x辆汽车,由题意知,每辆汽车的销售利润为$28-[27-0.1(x-1)]=(0.1x+0.9)$万元.当$0\leqslant x\leqslant 10$时,根据题意,得$x(0.1x+0.9)+0.5x=12$,整理,得$x^{2}+14x-120=0$,解得$x_{1}=-20$(不合题意,舍去),$x_{2}=6$.当$x＞10$时,根据题意,得$x(0.1x+0.9)+x=12$,整理,得$x^{2}+19x-120=0$,解得$x_{1}=-24$(不合题意,舍去),$x_{2}=5$.因为$5＜10$,所以$x=5$不合题意,需舍去.故需要售出6辆汽车.

6 (2025·连云港期中)某大学生利用暑假社会实践参与了一家网店经营,该网店以每个20元的价格购进900个某新型商品.第一周以每个35元的价格售出300个,第二周若按每个35元的价格销售仍可售出300个,但商店为了适当增加销量,决定降价销售(根据市场调查,单价每降低1元,可多售出50个).
(1)若第二周降低价格1元售出,则第一周、第二周分别获利多少元?
(2)若第二周单价降低x元销售一周后,商店对剩余商品清仓处理,以每个15元的价格全部售出,如果这批商品计划获利9500元,问第二周每个商品的单价应降低多少元?

答案：
(1)第一周获利:$300×(35-20)=4500$(元);第二周获利:$(300+50)×(35-1-20)=4900$(元).故第一周获利4500元,第二周获利4900元.
(2)根据题意,得$4500+(15-x)(300+50x)-5(900-300-300-50x)=9500$,即$x^{2}-14x+40=0$,解得$x_{1}=4,x_{2}=10$.当$x=4$时,$300+50x=500$,$500+300=800＜900$(符合题意);当$x=10$时,$300+50x=300+500=800$,$300+800=1100＞900$(不合题意,舍去).故第二周每个商品的销售价格应降价4元.

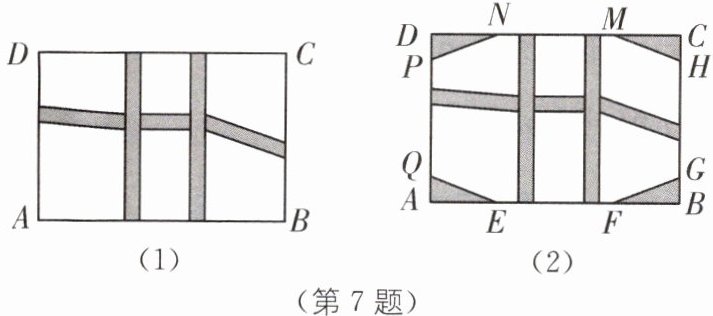
7 一题多问 (2024·江阴期中)某科研单位准备将院内一块长30米、宽20米的矩形ABCD空地,建成一个矩形花园,要求在花园内修两条纵向平行和一条横向弯折的小道(小道进出口的宽度相等,且每段小道均为平行四边形),剩余的地方种植花草.
(1)如图(1),要使种植花草的面积为532平方米,求小道进出口的宽度为多少米.
(2)现将矩形花园的四个角建成休闲活动区,如图(2)所示,△AEQ、△BGF、△CMH、△DPN均为全等的直角三角形,其中AE= BF= CM= DN,设EF= HG= MN= PQ= a米,竖向道路出口和横向弯折道路出口的宽度都为2米,且竖向道路出口位于MN和EF之间,横向弯折道路出口位于PQ和HG之间.
①求剩余的种植花草区域的面积(用含有a的代数式表示);
②如果种植花草区域的建造成本是100元/平方米,建造花草区域的总成本为42000元,求a的值.

答案：
(1)设小道进出口的宽度为x米,依题意,得$(30-2x)\cdot(20-x)=532$,整理,得$x^{2}-35x+34=0$,解得$x_{1}=1$,$x_{2}=34$.
∵$34＞20$,不合题意,舍去,
∴$x=1$.即小道进出口的宽度应为1米.
(2)①剩余的种植花草区域的面积$=(30-2× 2)×(20-2)-4×\frac{1}{2}(30-a)×\frac{1}{2}×\frac{1}{2}(20-a)=(-\frac{1}{2}a^{2}+25a+168)$平方米.
②根据题意,得$100(-\frac{1}{2}a^{2}+25a+168)=42000$,解得$a=14$或$a=36$(不合题意,舍去).故a的值为14.