《2025年课时训练九年级数学上册苏科版江苏人民出版社》

6 如图,甲、乙两人分别从正方形花坛ABCD的顶点B、C同时出发,甲由点B沿BC向点C运动,乙由点C沿CD向点D运动,甲的速度为2米/分,乙的速度为1米/分,当甲到达点C时甲、乙同时停止运动.若正方形花坛的周长为40米,问几分钟后,两人相距$2\sqrt {10}$米?

答案：
设x分钟后，两人相距2√10米。如图，设此时甲运动到点E，乙运动到点F。
∵正方形花坛ABCD的周长为40米，
∴BC=CD=10米。
∴FC=x米，EC=(10 - 2x)米。在Rt△EFC中，由勾股定理，得x²+(10 - 2x)²=(2√10)²，解得x₁=2，x₂=6。
∵甲由点B运动到点C的时间为10÷2=5(分钟)，
∴x=6应舍去。故2分钟后，两人相距2√10米。

(1)$PB=$(6 - t)cm,$QC=$(12 - 2t)cm.
(2)∵AP=t cm，QB=2t cm，PB=(6 - t)cm，CQ=(12 - 2t)cm，由题意可得S△DPQ=S矩形ABCD - S△APD - S△BPQ - S△DCQ=28，
∴AB·BC - 1/2 AP·AD - 1/2·PB·BQ - 1/2 CQ·CD=28，
∴12×6 - 1/2×12t - 1/2×2t×(6 - t) - 1/2×6×(12 - 2t)=28，
∴t² - 6t + 8=0，解得t₁=2，t₂=4。故t的值为2或4时，△DPQ的面积等于28 cm²。

答案：
(1)(6 - t)cm (12 - 2t)cm [解析]AP=t cm，QB=2t cm，
∴PB=(6 - t)cm，QC=(12 - 2t)cm。
(2)
∵AP=t cm，QB=2t cm，PB=(6 - t)cm，CQ=(12 - 2t)cm，由题意可得S△DPQ=S矩形ABCD - S△APD - S△BPQ - S△DCQ=28，
∴AB·BC - 1/2 AP·AD - 1/2·PB·BQ - 1/2 CQ·CD=28，
∴12×6 - 1/2×12t - 1/2×2t×(6 - t) - 1/2×6×(12 - 2t)=28，
∴t² - 6t + 8=0，解得t₁=2，t₂=4。故t的值为2或4时，△DPQ的面积等于28 cm²。

8 中考新考法 满足条件的结论开放如图,在矩形ABCD中,$AB= 6cm,BC= 8cm$,点P从点A沿边AB以2cm/s的速度向点B移动,同时点Q从点B沿边BC以1cm/s的速度向点C移动,当P、Q两点中有一个点到终点时,另一个点也会停止运动.当$\triangle DPQ$为直角三角形时,求点P运动的时间.

答案： 在矩形ABCD中，DC=AB=6 cm，AD=BC=8 cm，设运动时间为t s，则AP=2t cm，BQ=t cm，
∴PB=(6 - 2t)cm，CQ=(8 - t)cm。
∵∠A=90°，
∴PD²=8²+(2t)²。同理PQ²=(6 - 2t)²+t²，QD²=6²+(8 - t)²。当△DPQ为直角三角形时，∠DPQ=90°或∠DQP=90°。当∠DPQ=90°时，PD²+PQ²=QD²，即8²+(2t)²+(6 - 2t)²+t²=6²+(8 - t)²，整理，得t² - t=0，解得t₁=1，t₂=0(舍去)；当∠DQP=90°时，QD²+PQ²=PD²，即6²+(8 - t)²+(6 - 2t)²+t²=8²+(2t)²，整理，得t² - 20t + 36=0，解得t₁=2，t₂=18(舍去)。综上，当△DPQ为直角三角形时，点P的运动时间为1 s或2 s。

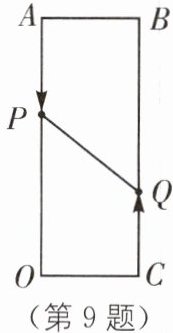
9 中考新考法 满足结论的条件开放(1)问题情境:如图,已知矩形AOCB,$AB= 6cm,BC= 16cm,$动点P从点A出发,沿边AO以3cm/s的速度向点O运动,直到点O为止;动点Q同时从点C出发,沿边CB以2cm/s的速度向点B运动,与点P同时结束运动,出发____时,点P和点Q之间的距离是10cm.
(2)逆向发散:当运动时间为2s时,P、Q两点的距离为多少?当运动时间为4s时,P、Q两点的距离为多少?
(3)拓展应用:若点P沿着$AO→OC→CB$移动,点P、Q分别从A、C同时出发,点Q从点C移动到点B停止时,点P随点Q的停止而停止移动,求经过多长时间$\triangle POQ的面积为12cm^{2}$?

答案：

(1)8/5 s或24/5 s [解析]如图，过点P作PE⊥BC于点E，设运动时间为t秒，则AP=3t cm，CQ=2t cm，PE=6 cm，EQ=16 - 3t - 2t=(16 - 5t)cm或EQ=3t+2t - 16=(5t - 16)cm。
∵点P和点Q之间的距离是10 cm，
∴6²+(16 - 5t)²=100，
∴t=8/5 s或t=24/5 s。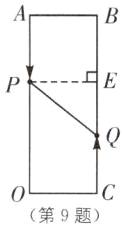
(2)由运动知，AP=3×2=6(cm)，CQ=2×2=4(cm)。
∵四边形APEB是矩形，
∴PE=AB=6 cm，BE=6 cm，
∴EQ=BC - BE - CQ=16 - 6 - 4=6(cm)。根据勾股定理，得当t=2 s时，P、Q两点的距离为6√2 cm。同理，当t=4 s时，P、Q两点的距离为2√13 cm。
(3)当点P在AO上时，S△POQ=1/2 PO·CO=1/2(16 - 3t)·6=12，解得t=4；当点P在OC上时，S△POQ=1/2 PO·CQ=1/2(3t - 16)·2t=12，解得t=6或t=-2/3(舍去)；当点P在CB上时，S△POQ=1/2 PQ·CO=1/2(2t+22 - 3t)·6=12，解得t=18＞8(不符合题意，舍去)。综上所述，经过4 s或6 s时，△POQ的面积为12 cm²。