《2025年课时训练九年级数学上册苏科版江苏人民出版社》

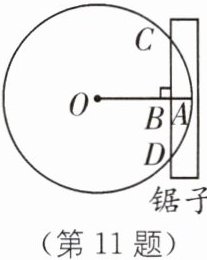
11 传统文化《九章算术》 (2024·苏州期末)《九章算术》中有这样一道题：“今有圆材埋于壁中,不知大小。以锯锯之,深一寸,锯道长一尺。问径几何?”其大意为：今有一圆柱形木材埋在墙壁中,不知其大小。设其横截面为⊙O,用锯子去锯这个木材,锯口深AB为1寸,锯道长CD为1尺。由此可得这块圆柱形木材横截面的直径是____尺。(注：1尺= 10寸)

答案：
2.6　[解析]如图,连接OC,由题意,得B为CD的中点,O、B、A三点共线,OA⊥CD,
∴BD=BC=$\frac{1}{2}$CD=5寸，设圆O的半径为x寸，则OB=(x−1)寸.在Rt△OBC中,由勾股定理得5²+(x−1)²=x²,解得x=13,
∴圆材半径为13寸，
∴圆材直径为2.6尺.
　　　　　　　　　　　　　　　　　

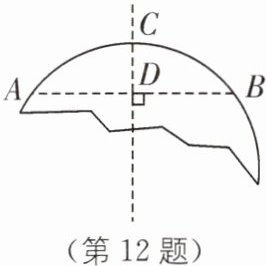
12 (2025·陕西西安期末)王师傅要测量一个如图所示的残缺圆形工件的半径,因为无法直接测量,所以王师傅这样操作：在工件圆弧上任取两点A、B,连接AB,作AB的垂直平分线CD交AB于点D,交$\overset{\frown}{AB}$于点C,测出AB= 40cm,CD= 10cm,便可求出该工件的半径,则该圆形工件的半径为25cm。

答案： 25

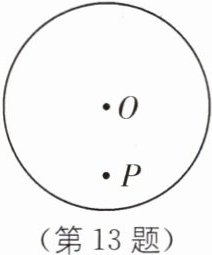
13 如图,点P是⊙O内一点。
(1)过点P画弦AB,使点P是AB的中点,并简述作图过程；
(2)连接OP并延长交⊙O于点C,若AB= 8,PC= 2,求⊙O的半径。

答案：
(1)①过点P作直径DE交⊙O于点D和E;②过点P作弦AB⊥DE交于点P.
(2)连接OA.设⊙O的半径为r,则OP=r−2.
∵OP⊥AB,
∴AP=$\frac{1}{2}$AB=$\frac{1}{2}$×8=4.
　　根据勾股定理，得OA²=AP²+OP²,
∴r²=4²+(r−2)²,解得r=5.
　　故⊙O的半径为5.

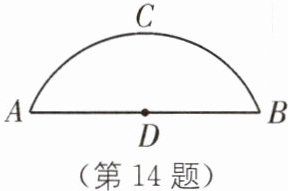
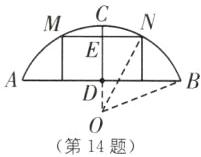
14 如图,有一座圆弧形拱桥,桥下水面宽度AB为12m,拱高CD为4m。
(1)求拱桥的半径。
(2)有一艘宽5m的货船,船舱顶部为长方形,并高出水面3.6m,问：此货船是否能顺利通过拱桥?

答案：

(1)如图，设圆心为O,连接OB、OC.
　　由题意，易知OC⊥AB,
∴D为AB的中点
∵AB=12m,
　　　　　　　　　　　　　　　
∴BD=$\frac{1}{2}$AB=6m.
　　又CD=4m,设OB=OC=r m,则OD=(r−4)m.
　　在Rt△BOD中,根据勾股定理,得r²=(r−4)²+6²,解得r=6.5.故拱桥的半径为6.5m.
(2)不能,理由如下:如图，连接ON.
∵CD=4m,船舱顶部为长方形并高出水面3.6m,
∴CE=4−3.6=0.4(m),
∴OE=r−CE=6.5−0.4=6.1(m),
　　在Rt△OEN中,EN²=ON²−OE²=6.5²−6.1²=5.04,
∴EN=$\sqrt{5.04}$m.
∴MN=2EN=2×$\sqrt{5.04}$≈4.49(m)＜5m.
　　故此货船不能顺利通过这座拱桥.

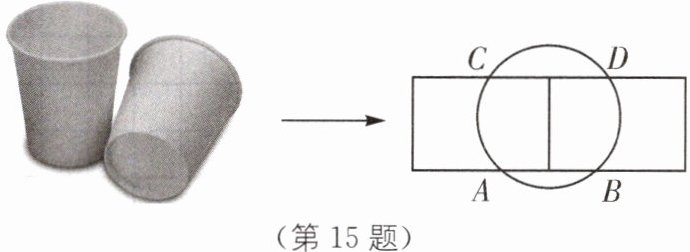
15 新情境 数学与生活融合 (2024·常州期中)一次综合实践的主题为：只用一张矩形纸条和刻度尺,如何测量一次性纸杯杯口的直径?小明同学所在的学习小组想到了如下方法：如图,将纸条拉直紧贴杯口上,纸条的上下边沿分别与杯口相交于A、B、C、D四点,利用刻度尺量得该纸条宽为3.5cm,AB= 3cm,CD= 4cm。请你帮忙计算纸杯的直径。

答案：
如图,MN⊥AB,MN过圆心O,连接OD、OB,
∴MN=3.5cm.
∵CD//AB,
∴MN⊥CD,
∴DM=$\frac{1}{2}$CD=$\frac{1}{2}$×4=2(cm),BN=$\frac{1}{2}$AB=$\frac{1}{2}$×3 =1.5(cm).设OM=xcm,则ON=MN−OM=(3.5−x)cm.
∵OM²+MD²=OD²,ON²+BN²=OB²,
∴OM²+MD²=ON²+BN²,
∴x²+2²=(3.5−x)²+1.5²,解得x=1.5,
∴OM=1.5cm,
∴OD=$\sqrt{OM²+MD²}$=$\sqrt{1.5²+2²}$=2.5(cm),
∴纸杯的直径为2.5×2=5(cm).