《2025年课时训练九年级数学上册苏科版江苏人民出版社》

(1)求这组数据的中位数.已知这组数据的均数为9.2 t,你对它与中位数的差异有什么看法?
共有100个数，按大小顺序排列后第50、51个数据分别是6.4、6.8，所以中位数为(6.4 + 6.8)÷2 = 6.6(t)。已知这组数据的平均数为9.2t，从平均数与中位数的差异可得大部分居民家庭去年的月均用水量小于平均数，有节约用水观念，少数家庭用水比较浪费。
(2)为了鼓励节约用水,要确定一个用水量的标准,超出这个标准的部分按1.5倍价格收费.若要使75%的家庭水费支出不受影响,你觉得这个标准应该定为多少?
∵100×75% = 75，第75个家庭去年的月均用水量为11t，∴为了鼓励节约用水，要使75%的家庭水费支出不受影响，则家庭月均用水量应该定为11t。故这个标准应该定为11t。

答案：
(1)共有100个数，按大小顺序排列后第50、51个数据分别是6.4、6.8，所以中位数为(6.4 + 6.8)÷2 = 6.6(t)。已知这组数据的平均数为9.2t，
∴从平均数与中位数的差异可得大部分居民家庭去年的月均用水量小于平均数，有节约用水观念，少数家庭用水比较浪费。
(2)
∵100×75% = 75，第75个家庭去年的月均用水量为11t，
∴为了鼓励节约用水，要使75%的家庭水费支出不受影响，则家庭月均用水量应该定为11t。故这个标准应该定为11t。

13 (2024·绵阳中考)某市射击队将从甲、乙两名运动员中选拔一人参加全省比赛,现对他们进行了6次测试,成绩(单位:环)统计如下:

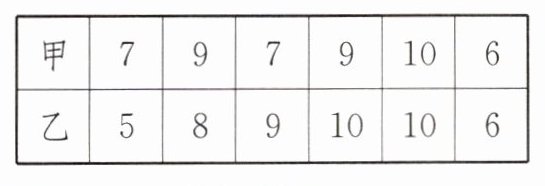
(1)根据表格中的数据填空:
甲的平均成绩是8环,乙的平均成绩是8环;甲成绩的中位数是8环,乙成绩的众数是10环;
(2)求甲、乙测试成绩的方差;
$s^{2}_{甲}=\frac{1}{6}×[(7 - 8)^{2}×2+(9 - 8)^{2}×2+(10 - 8)^{2}+(6 - 8)^{2}]=2$；$s^{2}_{乙}=\frac{1}{6}×[(5 - 8)^{2}+(8 - 8)^{2}+(9 - 8)^{2}+2×(10 - 8)^{2}+(6 - 8)^{2}]=\frac{11}{3}$。
(3)你认为推荐谁参加全省比赛更合适,请说明理由.
推荐甲参加全省比赛更合适，理由如下：因为两人的平均数相同，但甲的方差比乙小，即甲比乙更稳定，所以推荐甲参加全省比赛更合适。

答案：
(1)8 8 8 10 ［解析］
(1)甲的平均成绩是$\frac{1}{6}×(7×2+9×2+10+6)=8$(环)，乙的平均成绩是$\frac{1}{6}×(5+8+9+10×2+6)=8$(环)，甲成绩的中位数是$\frac{7+9}{2}=8$(环)，乙成绩的众数是10环。
(2)$s^{2}_{甲}=\frac{1}{6}×[(7 - 8)^{2}×2+(9 - 8)^{2}×2+(10 - 8)^{2}+(6 - 8)^{2}]=2$；$s^{2}_{乙}=\frac{1}{6}×[(5 - 8)^{2}+(8 - 8)^{2}+(9 - 8)^{2}+2×(10 - 8)^{2}+(6 - 8)^{2}]=\frac{11}{3}$。
(3)推荐甲参加全省比赛更合适，理由如下：因为两人的平均数相同，但甲的方差比乙小，即甲比乙更稳定，所以推荐甲参加全省比赛更合适。

14 在一次中学生田径运动会上,根据参加男子跳高初赛的运动员的成绩(单位:m),绘制出如图所示的统计图(1)和图(2),请根据相关信息,解答下列问题:
(1)图(1)中a的值为25;
(2)求统计的这组初赛成绩数据的平均数、众数和中位数;
(2)$\overline{x}=(1.50×2+1.55×4+1.60×5+1.65×6+1.70×3)÷(2+4+5+6+3)=1.61$(m)。
∵在这组数据中，1.65出现了6次，出现的次数最多，
∴这组数据的众数是1.65m。将这组数据从小到大排列，其中处于中间的两个数都是1.60，则这组数据的中位数是1.60m。
(3)根据这组初赛成绩,由高到低确定9人进入复赛,请直接写出初赛成绩为1.65 m的运动员能否进入复赛.
(3)能。初赛成绩不低于1.65m的运动员有9名，按初赛成绩由高到低确定进入复赛的有9名运动员，
∴初赛成绩为1.65m的运动员一定能进入复赛。

答案：
(1)25
(2)$\overline{x}=(1.50×2+1.55×4+1.60×5+1.65×6+1.70×3)÷(2+4+5+6+3)=1.61$(m)。
∵在这组数据中，1.65出现了6次，出现的次数最多，
∴这组数据的众数是1.65m。将这组数据从小到大排列，其中处于中间的两个数都是1.60，则这组数据的中位数是1.60m。
(3)能。初赛成绩不低于1.65m的运动员有9名，按初赛成绩由高到低确定进入复赛的有9名运动员，
∴初赛成绩为1.65m的运动员一定能进入复赛。