第40页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
18 (2025·盐城建湖期中)已知关于$x的一元二次方程x^{2}-(m+4)x+m+3= 0$。
(1)求证:无论实数$m$取何值,方程总有两个实数根;
(2)若方程两个根均为正整数,求负整数$m$的值。
(1)求证:无论实数$m$取何值,方程总有两个实数根;
(2)若方程两个根均为正整数,求负整数$m$的值。
答案:
(1)
∵Δ=(m+4)²-4(m+3)=(m+2)²≥0,
∴无论实数m取何值,方程总有两个实数根.
(2)x²-(m+4)x+m+3=0,
原方程可变形为(x-1)[x-(m+3)]=0.
解得x₁=1,x₂=m+3,
∵方程两个根均为正整数,
∴m+3>0,即m>-3.
∵m是负整数,
∴m=-1或-2.
(1)
∵Δ=(m+4)²-4(m+3)=(m+2)²≥0,
∴无论实数m取何值,方程总有两个实数根.
(2)x²-(m+4)x+m+3=0,
原方程可变形为(x-1)[x-(m+3)]=0.
解得x₁=1,x₂=m+3,
∵方程两个根均为正整数,
∴m+3>0,即m>-3.
∵m是负整数,
∴m=-1或-2.
19 中考新考法 满足条件的结论开放 已知关于$x的一元二次方程x^{2}-(m+5)x+5m= 0$。
(1)若此方程的一个根是$x= 2$,求方程的另一根;
(2)求证:这个一元二次方程一定有两个实数根;
(3)设该一元二次方程的两根为$a$、$b$,且2、$a$、$b$分别是一个直角三角形的三边长,求$m$的值。
(1)若此方程的一个根是$x= 2$,求方程的另一根;
(2)求证:这个一元二次方程一定有两个实数根;
(3)设该一元二次方程的两根为$a$、$b$,且2、$a$、$b$分别是一个直角三角形的三边长,求$m$的值。
答案:
(1)设方程的另一个根为t,
根据根与系数的关系,得2+t=m+5,2t=5m,
∴2t=5(t-3),解得t=5,即方程的另一个根为5.
(2)
∵Δ=(m+5)²-4×5m=m²-10m+25=(m-5)²≥0,
∴这个一元二次方程一定有两个实数根.
(3)解方程x²-(m+5)x+5m=0,得x₁=5,x₂=m,即a=5,b=m或a=m,b=5.
∵2、a、b分别是一个直角三角形的三边长,
∴2²+m²=5²或2²+5²=m².
解方程2²+m²=5²,得m₁=$\sqrt{21}$,m₂=-$\sqrt{21}$(舍去),
解方程2²+5²=m²,得m₁=$\sqrt{29}$,m₂=-$\sqrt{29}$(舍去).
故m的值为$\sqrt{21}$或$\sqrt{29}$.
(1)设方程的另一个根为t,
根据根与系数的关系,得2+t=m+5,2t=5m,
∴2t=5(t-3),解得t=5,即方程的另一个根为5.
(2)
∵Δ=(m+5)²-4×5m=m²-10m+25=(m-5)²≥0,
∴这个一元二次方程一定有两个实数根.
(3)解方程x²-(m+5)x+5m=0,得x₁=5,x₂=m,即a=5,b=m或a=m,b=5.
∵2、a、b分别是一个直角三角形的三边长,
∴2²+m²=5²或2²+5²=m².
解方程2²+m²=5²,得m₁=$\sqrt{21}$,m₂=-$\sqrt{21}$(舍去),
解方程2²+5²=m²,得m₁=$\sqrt{29}$,m₂=-$\sqrt{29}$(舍去).
故m的值为$\sqrt{21}$或$\sqrt{29}$.
20 某商店销售甲、乙两种零食,甲零食每袋成本为5元,乙零食每袋成本为7元。甲零食现在的售价为10元,每天卖出30袋;售价每提高1元,每天少卖出2袋。乙零食现在的售价为14元,每天卖出6袋;售价每降低1元,每天多卖出4袋。假定甲、乙两种零食每天卖出的袋数的和不变(和为36袋),且售价均为整数。
(1)当甲零食的售价提高2元,则甲零食每天卖出
(2)当甲零食的售价提高多少元时,销售这两种零食当天的总利润是268元?
设甲零食的售价提高x元,
由题意,得(10+x-5)(30-2x)+[36-(30-2x)]·($\frac{14-2x}{4}$-7)=268,
整理,得(x-4)(3x-19)=0,
解得x₂=4,x₂=$\frac{19}{3}$(舍去).
故当甲零食的售价提高4元时,销售这两种零食当天的总利润是268元.
(1)当甲零食的售价提高2元,则甲零食每天卖出
26
袋,乙零食的售价为13
元。(2)当甲零食的售价提高多少元时,销售这两种零食当天的总利润是268元?
设甲零食的售价提高x元,
由题意,得(10+x-5)(30-2x)+[36-(30-2x)]·($\frac{14-2x}{4}$-7)=268,
整理,得(x-4)(3x-19)=0,
解得x₂=4,x₂=$\frac{19}{3}$(舍去).
故当甲零食的售价提高4元时,销售这两种零食当天的总利润是268元.
答案:
(1)26 13
(2)设甲零食的售价提高x元,
由题意,得(10+x-5)(30-2x)+[36-(30-2x)]·($\frac{14-2x}{4}$-7)=268,
整理,得(x-4)(3x-19)=0,
解得x₂=4,x₂=$\frac{19}{3}$(舍去).
故当甲零食的售价提高4元时,销售这两种零食当天的总利润是268元.
(1)26 13
(2)设甲零食的售价提高x元,
由题意,得(10+x-5)(30-2x)+[36-(30-2x)]·($\frac{14-2x}{4}$-7)=268,
整理,得(x-4)(3x-19)=0,
解得x₂=4,x₂=$\frac{19}{3}$(舍去).
故当甲零食的售价提高4元时,销售这两种零食当天的总利润是268元.
21 (2025·连云港赣榆区期中)已知$x_{1}$、$x_{2}是方程x^{2}-x-3= 0$的两根,则$x_{1}^{2}+x_{2}^{2}= $
7
。
答案:
7 [解析]
∵x₁、x₂是方程x²-x-3=0的两根,
∴由一元二次方程根与系数的关系得x₁+x₂=1,x₁·x₂=-3.
∴x₁²+x₂²=(x₁+x₂)²-2x₁x₂=1²-2×(-3)=7.
思路引导 熟练运用一元二次方程解的定义及根与系数的关系是解决问题的关键.
∵x₁、x₂是方程x²-x-3=0的两根,
∴由一元二次方程根与系数的关系得x₁+x₂=1,x₁·x₂=-3.
∴x₁²+x₂²=(x₁+x₂)²-2x₁x₂=1²-2×(-3)=7.
思路引导 熟练运用一元二次方程解的定义及根与系数的关系是解决问题的关键.
22 (2024·深圳模拟)社区利用一块矩形空地$ABCD$建了一个小型停车场,其布局如图所示。已知$AD= 52m$,$AB= 28m$,阴影部分设计为停车位,要铺花砖,其余部分均为宽度为$x m$的道路。已知铺花砖的面积为$640m^{2}$。
(1)道路的宽是多少米?
(2)该停车场共有车位50个,据调查分析,当每个车位的月租金为200元时,可全部租出;若每个车位的月租金每上涨5元,就会少租出1个车位。当每个车位的月租金上涨多少元时,停车场的月租金收入为10125元?
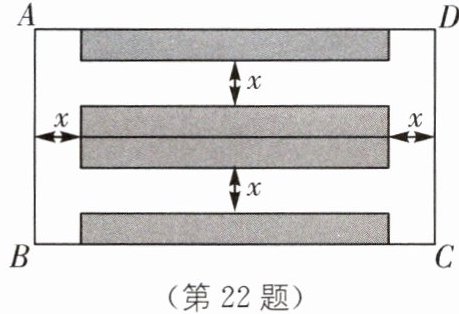
(1)道路的宽是多少米?
(2)该停车场共有车位50个,据调查分析,当每个车位的月租金为200元时,可全部租出;若每个车位的月租金每上涨5元,就会少租出1个车位。当每个车位的月租金上涨多少元时,停车场的月租金收入为10125元?

答案:
(1)若道路的宽为x米,根据题意,得(52-2x)(28-2x)=640,
整理,得x²-40x+204=0,
解得x₁=34(舍去),x₂=6.
故道路的宽为6米.
(2)设月租金上涨a元时,停车场的月租金收入为10125元,
根据题意,得(200+a)(50-$\frac{a}{5}$)=10125,
整理,得a²-50a+625=0,解得a₁=a₂=25.
故每个车位的月租金上涨25元时,停车场的月租金收入为10125元.
(1)若道路的宽为x米,根据题意,得(52-2x)(28-2x)=640,
整理,得x²-40x+204=0,
解得x₁=34(舍去),x₂=6.
故道路的宽为6米.
(2)设月租金上涨a元时,停车场的月租金收入为10125元,
根据题意,得(200+a)(50-$\frac{a}{5}$)=10125,
整理,得a²-50a+625=0,解得a₁=a₂=25.
故每个车位的月租金上涨25元时,停车场的月租金收入为10125元.
查看更多完整答案,请扫码查看


