第74页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
7 在平面直角坐标系中,直线$y=\frac{3}{4}x+3$与$x$轴、$y$轴分别交于$A$、$B$两点,$\odot F$与$x$轴、$y$轴和直线$AB$分别相切于点$D$、$E$、$C$,求$\odot F$的半径。
答案:
∵直线y = 3/4 x + 3与x轴、y轴分别交于A、B两点,
∴点A的坐标为(-4,0),点B的坐标为(0,3),
∴OA=4,OB=3.
∵∠AOB=90°,
∴S△OAB = 1/2 OA·OB = 6,AB = √(OA² + OB²)=5.
①若点F在如图
(1)的位置,设⊙F的半径为r,连接FA、FB、FO、FD、FE、FC,则FD=FE=FC=r.

∵⊙F与x轴、y轴和直线AB分别相切于点D(0,3),E、C,
∴FD⊥OA,FE⊥OB,FC⊥AB.
∵S△OAB = S△OAF + S△OBF + S△ABF,
∴6 = 1/2 OA·FD + 1/2 OB·FE + 1/2 AB·FC,
∴6 = 1/2 r(OA + OB + AB)=1/2 r×(4 + 3 + 5),
∴r = 1.
②若点F在如图
(2)的位置,设⊙F的半径为r,连接FA、FB、FO、FD、FE、FC,则FD=FE=FC=r.

∵⊙F与x轴、y轴和直线AB分别相切于点D、E、C,
∴FD⊥OA,FE⊥OB,FC⊥AB.
∵S△OAB = S△OAF + S△ABF - S△OBF,
∴6 = 1/2 OA·FD + 1/2 AB·FC - 1/2 OB·FE,
∴6 = 1/2 r(OA + AB - OB)=1/2 r×(4 + 5 - 3),
∴r = 2.
③若点F在如图
(3)的位置,设⊙F的半径为r,连接FA、FB、FO、FD、FE、FC,则FD=FE=FC=r.

∵⊙F与x轴、y轴和直线AB分别相切于点D、E、C,
∴FD⊥OA,FE⊥OB,FC⊥AB.
∵S△OAB = S△OBF + S△ABF - S△OAF,
∴6 = 1/2 OB·FE + 1/2 AB·FC - 1/2 OA·FD,
∴6 = 1/2 r(OB + AB - OA)=1/2 r×(3 + 5 - 4),
∴r = 3.
④若点F在如图
(4)的位置,设⊙F的半径为r,连接FA、FB、FO、FD、FE、FC,则FD=FE=FC=r.

∵⊙F与x轴、y轴和直线AB分别相切于点D、E、C,
∴FD⊥OA,FE⊥OB,FC⊥AB.
∵S△OAB = S△OAF + S△OBF - S△ABF,
∴6 = 1/2 OA·FD + 1/2 OB·FE - 1/2 AB·FC,
∴6 = 1/2 r(OA + OB - AB)=1/2 r×(4 + 3 - 5),
∴r = 6.综上,满足条件的⊙F的半径为1或2或3或6.
∵直线y = 3/4 x + 3与x轴、y轴分别交于A、B两点,
∴点A的坐标为(-4,0),点B的坐标为(0,3),
∴OA=4,OB=3.
∵∠AOB=90°,
∴S△OAB = 1/2 OA·OB = 6,AB = √(OA² + OB²)=5.
①若点F在如图
(1)的位置,设⊙F的半径为r,连接FA、FB、FO、FD、FE、FC,则FD=FE=FC=r.

∵⊙F与x轴、y轴和直线AB分别相切于点D(0,3),E、C,
∴FD⊥OA,FE⊥OB,FC⊥AB.
∵S△OAB = S△OAF + S△OBF + S△ABF,
∴6 = 1/2 OA·FD + 1/2 OB·FE + 1/2 AB·FC,
∴6 = 1/2 r(OA + OB + AB)=1/2 r×(4 + 3 + 5),
∴r = 1.
②若点F在如图
(2)的位置,设⊙F的半径为r,连接FA、FB、FO、FD、FE、FC,则FD=FE=FC=r.

∵⊙F与x轴、y轴和直线AB分别相切于点D、E、C,
∴FD⊥OA,FE⊥OB,FC⊥AB.
∵S△OAB = S△OAF + S△ABF - S△OBF,
∴6 = 1/2 OA·FD + 1/2 AB·FC - 1/2 OB·FE,
∴6 = 1/2 r(OA + AB - OB)=1/2 r×(4 + 5 - 3),
∴r = 2.
③若点F在如图
(3)的位置,设⊙F的半径为r,连接FA、FB、FO、FD、FE、FC,则FD=FE=FC=r.

∵⊙F与x轴、y轴和直线AB分别相切于点D、E、C,
∴FD⊥OA,FE⊥OB,FC⊥AB.
∵S△OAB = S△OBF + S△ABF - S△OAF,
∴6 = 1/2 OB·FE + 1/2 AB·FC - 1/2 OA·FD,
∴6 = 1/2 r(OB + AB - OA)=1/2 r×(3 + 5 - 4),
∴r = 3.
④若点F在如图
(4)的位置,设⊙F的半径为r,连接FA、FB、FO、FD、FE、FC,则FD=FE=FC=r.

∵⊙F与x轴、y轴和直线AB分别相切于点D、E、C,
∴FD⊥OA,FE⊥OB,FC⊥AB.
∵S△OAB = S△OAF + S△OBF - S△ABF,
∴6 = 1/2 OA·FD + 1/2 OB·FE - 1/2 AB·FC,
∴6 = 1/2 r(OA + OB - AB)=1/2 r×(4 + 3 - 5),
∴r = 6.综上,满足条件的⊙F的半径为1或2或3或6.
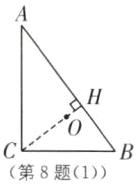
问题情境:数学活动课上,老师出示了一个直角三角板和量角器,把量角器的中心点$O$放置在$AC$的中点上,$DE$与直角边$AC$重合,如图(1)所示,$∠C=90^{\circ}$,$BC=6$,$AC=8$,$OD=3$,量角器交$AB$于点$G$,$F$,现将量角器$DE$绕点$C$旋转,如图(2)所示。
(1)点$C$到边$AB$的距离为____;
(2)在旋转过程中,求点$O$到$AB$距离的最小值;
(3)若半圆$O$与$Rt\triangle ABC$的直角边相切,设切点为$K$,求$BK$的长。

(1)点$C$到边$AB$的距离为____;
(2)在旋转过程中,求点$O$到$AB$距离的最小值;
(3)若半圆$O$与$Rt\triangle ABC$的直角边相切,设切点为$K$,求$BK$的长。

答案:
8.
(1)24/5 [解析]如图
(1),过点C作CH⊥AB于点H,
∵∠ACB = 90°,BC = 6,AC = 8,
∴AB = √(AC² + BC²)=√(6² + 8²)=10.
∵CH⊥AB,
∴AB·CH = AC·BC,
∴CH = (AC·BC)/AB=(6×8)/10 = 24/5,即点C到边AB的距离为24/5.
(2)
∵O为AC的中点,
∴OC = 1/2 AC = 1/2×8 = 4,当CD⊥AB时,点O到AB的距离最小,
∴OH = CH - OC = 24/5 - 4 = 4/5,
∴点O到AB距离的最小值为4/5.
(3)①当半圆O与BC相切时,如图
(2),设切点为K,连接OK,
∴∠OKC = 90°,在Rt△OCK中,OK = 3,OC = 4,
∴CK = √(OC² - OK²)=√(4² - 3²)=√7,
∴BK = BC - CK = 6 - √7;
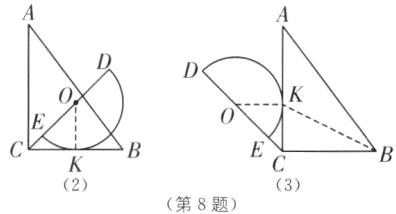
②当半圆O与AC相切时,如图
(3),设切点为K,连接OK,
∴∠OKC = 90°.在Rt△OCK中,OK = 3,OC = 4,
∴CK = √(OC² - OK²)=√(4² - 3²)=√7,在Rt△BCK中,BK = √(BC² + CK²)=√(6²+(√7)²)=√43.综上所述,BK 的长为6 - √7或√43.
8.
(1)24/5 [解析]如图
(1),过点C作CH⊥AB于点H,
∵∠ACB = 90°,BC = 6,AC = 8,
∴AB = √(AC² + BC²)=√(6² + 8²)=10.
∵CH⊥AB,
∴AB·CH = AC·BC,
∴CH = (AC·BC)/AB=(6×8)/10 = 24/5,即点C到边AB的距离为24/5.

(2)
∵O为AC的中点,
∴OC = 1/2 AC = 1/2×8 = 4,当CD⊥AB时,点O到AB的距离最小,
∴OH = CH - OC = 24/5 - 4 = 4/5,
∴点O到AB距离的最小值为4/5.
(3)①当半圆O与BC相切时,如图
(2),设切点为K,连接OK,
∴∠OKC = 90°,在Rt△OCK中,OK = 3,OC = 4,
∴CK = √(OC² - OK²)=√(4² - 3²)=√7,
∴BK = BC - CK = 6 - √7;

②当半圆O与AC相切时,如图
(3),设切点为K,连接OK,
∴∠OKC = 90°.在Rt△OCK中,OK = 3,OC = 4,
∴CK = √(OC² - OK²)=√(4² - 3²)=√7,在Rt△BCK中,BK = √(BC² + CK²)=√(6²+(√7)²)=√43.综上所述,BK 的长为6 - √7或√43.
9 中考新考法 满足条件的结论开放 如图(1),在矩形$ABCD$中,$AB=6cm$,$BC=8cm$,点$P$以$3cm/s$的速度从点$A$向点$B$运动,点$Q$以$4cm/s$的速度从点$C$向点$B$运动。点$P$、$Q$同时出发,运动时间为$t\ s(0<t<2)$,$\odot M$是$\triangle PQB$的外接圆。
(1)当$t=1$时,$\odot M$的半径是____$cm$,$\odot M$与直线$CD$的位置关系是____;
(2)在点$P$从点$A$向点$B$运动过程中,当$\odot M$与矩形$ABCD$的一条边相切时,求$t$的值;
(3)连接$PD$,交$\odot M$于点$N$,如图(2),当$∠APD=∠NBQ$时,$t$的值是____。

(1)当$t=1$时,$\odot M$的半径是____$cm$,$\odot M$与直线$CD$的位置关系是____;
(2)在点$P$从点$A$向点$B$运动过程中,当$\odot M$与矩形$ABCD$的一条边相切时,求$t$的值;
(3)连接$PD$,交$\odot M$于点$N$,如图(2),当$∠APD=∠NBQ$时,$t$的值是____。

答案:
9.
(1)5/2 相离 [解析]如图
(1),过点M作KN⊥AB于点N,交CD于点K.
∵四边形ABCD是矩形,
∴∠ABC = 90°,AB//CD,
∴⊙M的直径是PQ,KN⊥CD.当t = 1时,AP = 3cm,CQ = 4cm.
∵AB = 6cm,BC = 8cm,
∴PB = 6 - 3 = 3(cm),BQ = 8 - 4 = 4(cm),
∴在Rt△PBQ中,PQ = √(3² + 4²)=5(cm),
∴⊙M的半径为5/2cm.
∵MN//BQ,M是PQ的中点,
∴PN = BN,
∴MN是△PQB的中位线,
∴MN = 1/2 BQ = 2cm.
∴MK = 8 - 2 = 6(cm).又6>5/2,
∴⊙M与直线CD的位置关系是相离.

(2)如图
(2),当⊙M与AD相切时,设切点为F,连接FM并延长交BC于点E,则EF⊥AD,EF⊥BC.
∵BQ=(8 - 4t)cm,PB=(6 - 3t)cm,
∴PQ=(10 - 5t)cm,
∴PM = FM=(5 - 5t/2)cm.
∵EF⊥BC,
∴E为BQ的中点,
∴ME是△PQB的中位线,
∴ME = 1/2 PB=(3 - 3t/2)cm.
∵EF = FM + ME,
∴5 - 5t/2+3 - 3t/2 = 6,解得t = 1/2.如图
(3),当⊙M与CD相切时,设切点为E,连接EM并延长交AB于点F,则EF⊥CD,EF⊥AB.
∵BQ=(8 - 4t)cm,PB=(6 - 3t)cm,
∴PQ=(10 - 5t)cm,
∴PM = EM=(5 -5t/2)cm.
∵EF⊥BP,F为PB的中点,
∴MF是△PBQ的中位线,
∴MF = 1/2 BQ=(4 - 2t)cm.
∵EF = EM + MF,
∴5 - 5t/2+4 - 2t =8,解得t = 2/9.综上,t的值为1/2或2/9.
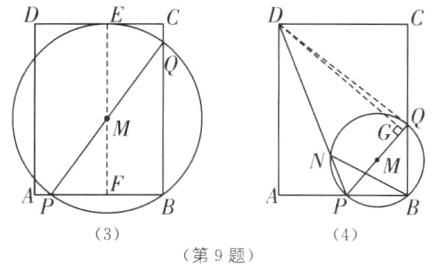
(3)4/3 [解析]如图
(4),过点D作DG⊥PQ,交直线PQ于点G,连接DQ.
∵∠APD = ∠NBQ,∠NBQ = ∠NPQ,
∴∠APD = ∠NPQ.
∵∠A = 90°,DG⊥PG,
∴AD = DG = 8cm.
∵PD = PD,
∴Rt△APD≌Rt△GPD(HL),
∴PG = AP = 3t.
∵PQ=(10 - 5t)cm,
∴QG = |10 - 5t - 3t| = |10 - 8t|cm.
∵DC² + CQ² = DQ² = DG² + QG²,
∴6²+(4t)² = 8²+(10 - 8t)²,
∴3t² - 10t + 8 = 0,(t - 2)(3t - 4)=0,解得t₁ = 2(舍去),t₂ = 4/3.
9.
(1)5/2 相离 [解析]如图
(1),过点M作KN⊥AB于点N,交CD于点K.
∵四边形ABCD是矩形,
∴∠ABC = 90°,AB//CD,
∴⊙M的直径是PQ,KN⊥CD.当t = 1时,AP = 3cm,CQ = 4cm.
∵AB = 6cm,BC = 8cm,
∴PB = 6 - 3 = 3(cm),BQ = 8 - 4 = 4(cm),
∴在Rt△PBQ中,PQ = √(3² + 4²)=5(cm),
∴⊙M的半径为5/2cm.
∵MN//BQ,M是PQ的中点,
∴PN = BN,
∴MN是△PQB的中位线,
∴MN = 1/2 BQ = 2cm.
∴MK = 8 - 2 = 6(cm).又6>5/2,
∴⊙M与直线CD的位置关系是相离.

(2)如图
(2),当⊙M与AD相切时,设切点为F,连接FM并延长交BC于点E,则EF⊥AD,EF⊥BC.
∵BQ=(8 - 4t)cm,PB=(6 - 3t)cm,
∴PQ=(10 - 5t)cm,
∴PM = FM=(5 - 5t/2)cm.
∵EF⊥BC,
∴E为BQ的中点,
∴ME是△PQB的中位线,
∴ME = 1/2 PB=(3 - 3t/2)cm.
∵EF = FM + ME,
∴5 - 5t/2+3 - 3t/2 = 6,解得t = 1/2.如图
(3),当⊙M与CD相切时,设切点为E,连接EM并延长交AB于点F,则EF⊥CD,EF⊥AB.
∵BQ=(8 - 4t)cm,PB=(6 - 3t)cm,
∴PQ=(10 - 5t)cm,
∴PM = EM=(5 -5t/2)cm.
∵EF⊥BP,F为PB的中点,
∴MF是△PBQ的中位线,
∴MF = 1/2 BQ=(4 - 2t)cm.
∵EF = EM + MF,
∴5 - 5t/2+4 - 2t =8,解得t = 2/9.综上,t的值为1/2或2/9.

(3)4/3 [解析]如图
(4),过点D作DG⊥PQ,交直线PQ于点G,连接DQ.
∵∠APD = ∠NBQ,∠NBQ = ∠NPQ,
∴∠APD = ∠NPQ.
∵∠A = 90°,DG⊥PG,
∴AD = DG = 8cm.
∵PD = PD,
∴Rt△APD≌Rt△GPD(HL),
∴PG = AP = 3t.
∵PQ=(10 - 5t)cm,
∴QG = |10 - 5t - 3t| = |10 - 8t|cm.
∵DC² + CQ² = DQ² = DG² + QG²,
∴6²+(4t)² = 8²+(10 - 8t)²,
∴3t² - 10t + 8 = 0,(t - 2)(3t - 4)=0,解得t₁ = 2(舍去),t₂ = 4/3.
查看更多完整答案,请扫码查看


