《2025年课时训练九年级数学上册苏科版江苏人民出版社》

1 下列说法正确的有(B).
A.经过圆心的线段是直径
B.直径是同一个圆中最长的弦
C.长度相等的两条弧是等弧
D.弧分为优弧和劣弧

答案： B

在$Rt△ABC$中,$∠ACB= 90^{\circ },AB= 5,BC= 4$.以点A为圆心,r为半径作圆,当点C在$\odot A$内且点B在$\odot A$外时,r的值可能是(B).
A.3
B.4
C.5
D.6

答案： B

3 如图,在平面直角坐标系xOy中,$\odot P$经过点O,与y轴交于点$A(0,6)$,与x轴交于点$B(8,0)$,则OP的长为____.

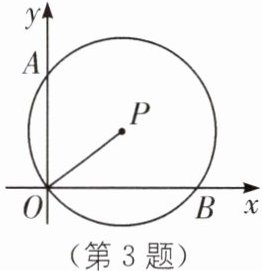
答案：
5 [解析]过点 P 作 PM⊥OB 于点 M，PN⊥OA 于点 N.
　　　　　　　　
∵∠MON=90°，
∴四边形 MONP 是矩形，
∴PM=ON.
∵A(0,6)，B(8,0)，
∴OA=6，OB=8，由垂径定理得 OM=MB= $\frac{1}{2}$OB=4，ON=NA= $\frac{1}{2}$OA=3，
∴PM=ON=3，
∴OP= $\sqrt{OM^2+PM^2}=\sqrt{4^2+3^2}=5$.

4 新情境 泥水平衡盾构机 (2024·南京建邺区期中)根据江心洲地质水文条件量身打造的“新时代号”泥水平衡盾构机,是目前世界上最先进的盾构设备之一,被誉为“国之重器”.如图(1),盾构机核心部件——刀盘的形状是一个圆形.如图(2),当机器暂停时,刀盘露在地上部分的跨度$AB= 12m$,拱高(弧的中点到弦的距离CD)3m,求盾构机刀盘的半径.

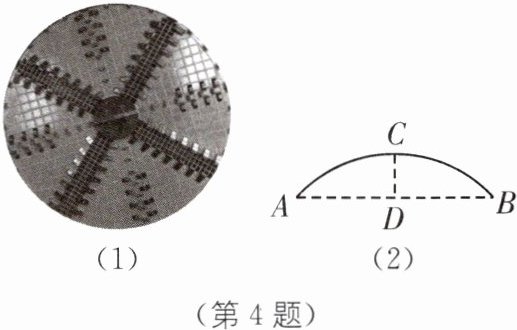
答案：
如图，设 OA=OC=r m.
∵OC⊥AB，
∴AD=DB= $\frac{1}{2}$AB=6 m.
　　　　　　　　　　　　　　　　
∵OA²=AD²+OD²，
∴r²=6²+(r-3)²，
∴r=7.5.故盾构机刀盘的半径为 7.5 m.

5 如图,在$Rt△ABC$中,$∠BAC= 90^{\circ },AB= 3,AC= 4$,在平面上有一点P,连接AP、CP,且$CP= 2$,取AP的中点M.连接BM,则BM的最小值为( ).

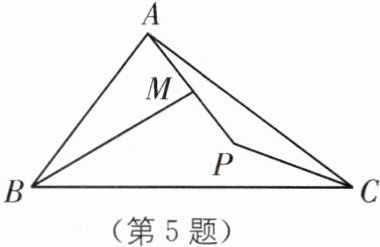
A.$\sqrt {10}$
B.$\frac {6\sqrt {5}}{5}$
C.$\sqrt {13}-1$
D.$2\sqrt {3}$

答案：
C [解析]如图，取 AC 的中点 N，连接 MN、BN.
∵AN=CN= $\frac{1}{2}$AC=2，
　　　　　　　　　　　　　　
∠BAN=90°，AB=3，
∴BN= $\sqrt{AB^2+AN^2}=\sqrt{3^2+2^2}=\sqrt{13}$.
∵AM=MP，AN=NC，
∴MN= $\frac{1}{2}$PC=1.
∵BM≥BN-MN，
∴BM≥ $\sqrt{13}-1$，
∴BM 的最小值为 $\sqrt{13}-1$.故选 C.

6 原创素养题 抽象能力 $△ABC$内接于半径为5的$\odot O$,且BC边长是6,则$△ABC$的面积最大值是____27.

答案： 27

7 如图,在平面直角坐标系中,已知点$A(1,0)$、$B(1-a,0)$、$C(1+a,0)(a＞0)$,点P在以$D(4,4)$为圆心,1为半径的圆上运动,且始终满足$∠BPC= 90^{\circ }$,则a的最大值是____.

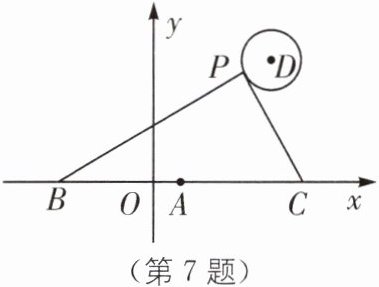
答案：
6 [解析]如图，连接 AP.
∵A(1,0)、B(1−a,0)、C(1+a,0)(a＞0)，
∴AB=1−(1−a)=a，CA=a+1−1=a，
∴AB=AC.
∵∠BPC=90°，
∴PA=AB=AC=a.
　连接 AD 并延长交⊙D 于点 P'，此时 AP'最长，
　　　　　　
∵A(1,0)、D(4,4)，
∴AD= $\sqrt{(4-1)^2+4^2}=5$，
∴AP'=5+1=6.故 a 的最大值为 6.

8 如图,已知$\odot O$的直径为26,弦$AB= 24$,动点P、Q在$\odot O$上,弦$PQ= 10$,若点M、N分别是弦AB、PQ的中点,则线段MN的取值范围是( ).

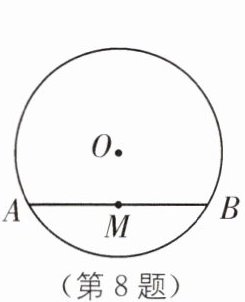
A.$7≤MN≤17$
B.$14≤MN≤34$
C.$7＜MN＜17$
D.$6≤MN≤16$

答案：
A [解析]如图，连接 OM、ON、OA、OP.
∵⊙O 的直径为 26，
∴OA=OP=13.
∵点 M、N 分别是弦 AB、PQ 的中点，AB=24，PQ=10，
∴OM⊥AB，ON⊥PQ，AM= $\frac{1}{2}$AB=12，PN= $\frac{1}{2}$PQ=5，
∴OM= $\sqrt{13^2-12^2}=5$，ON= $\sqrt{13^2-5^2}=12$.
　当 AB//PQ 时，M、O、N 三点共线，当 AB、PQ 位于 O 的同侧时，线段 MN 的长度最短=ON-OM=12-5=7，当 AB、PQ 位于 O 的两侧时，线段 MN 的长度最长=ON+OM=12+5=17，
∴线段 MN 的长度的取值范围是 7≤MN≤17.故选 A.
　　　　　　　　　　　　　　　　

9 如图,$\odot O在△ABC$三边上截得的弦长相等,即$DE= FG= MN,∠A= 50^{\circ }$,则$∠BOC$为( ).

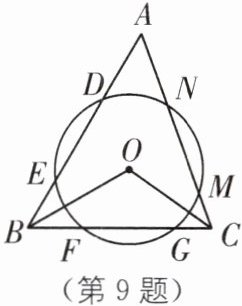
A.$100^{\circ }$
B.$110^{\circ }$
C.$115^{\circ }$
D.$120^{\circ }$

答案：
C [解析]如图，过点 O 作 OP⊥AB 于点 P，OQ⊥BC 于点 Q，OK⊥AC 于点 K，
∵DE=FG=MN，
∴OP=OK=OQ.
∴OB、OC 平分∠ABC 和∠ACB.
∴∠BOC=180°-(∠OBC+∠OCB)=180°- $\frac{1}{2}$(∠ABC+∠ACB)=180°- $\frac{1}{2}$(180°-∠A)=180°- $\frac{1}{2}$×(180°-50°)=115°.故选 C.