第62页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
1 (2025·无锡经开区期末)已知$\odot O$的半径为4,圆心O到直线l的距离为5,则直线l与$\odot O$的位置关系是(
A.相交
B.相切
C.相离
D.不能确定
C
).A.相交
B.相切
C.相离
D.不能确定
答案:
C
2 (教材P73习题T1·改编)已知$\odot O$的直径为10 cm,圆心O到直线l的距离为5 cm,则直线l与$\odot O$的位置关系是(
A.相离
B.相切
C.相交
D.相交或相切
B
).A.相离
B.相切
C.相交
D.相交或相切
答案:
B [解析]根据直线到圆心的距离等于半径,直线与圆相切。圆的直径为10cm,则半径为5cm,圆心到直线的距离为5cm,d = r,所以l与⊙O相切。故选B。
3 已知$\odot O$的半径为2,若点P是$\odot O$的切线l上任一点,则OP长的取值范围是______
OP≥2
.
答案:
OP≥2 [解析]根据切线与圆只有一个公共点在圆上,其他点在圆外,所以点P到圆心的距离大于或等于圆的半径,即OP≥2。
4 (2024·镇江京口区期中)已知点A(3,4),若以点A为圆心,3个单位长度为半径作圆,则$\odot A$与x轴的位置关系为
相离
.
答案:
相离
5 (教材P65例1·变式)如图,已知直线l与$\odot O$相交于A、B两点,点O到直线l的距离为3,AB= 8.
(1)求$\odot O$的直径.
(2)$\odot O$满足什么条件时,它与直线l不相交?

(1)求$\odot O$的直径.
(2)$\odot O$满足什么条件时,它与直线l不相交?

答案:
(1)作OD⊥AB于点D,连接OA,
∴AD = $\frac{1}{2}$AB = 4,∠ODA = 90°。
∵OD = 3,
∴AO = $\sqrt{4² + 3²}$ = 5,
∴⊙O的直径为10。
(2)⊙O的半径0<r≤3。
(1)作OD⊥AB于点D,连接OA,
∴AD = $\frac{1}{2}$AB = 4,∠ODA = 90°。
∵OD = 3,
∴AO = $\sqrt{4² + 3²}$ = 5,
∴⊙O的直径为10。
(2)⊙O的半径0<r≤3。
6 如图,AB是$\odot O$的直径,ED切$\odot O$于点C,AD交$\odot O$于点F,AC平分∠BAD,连接BF.
(1)求证:AD⊥ED;
(2)若CD= 4,AF= 2,求$\odot O$的半径.
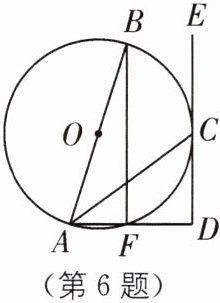
(1)求证:AD⊥ED;
(2)若CD= 4,AF= 2,求$\odot O$的半径.
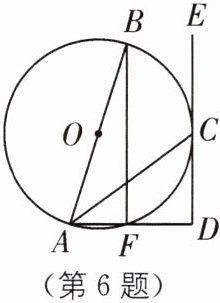
答案:
(1)如图,连接OC。
∵AC平分∠BAD,
∴∠1 = ∠2。
∵OA = OC,
∴∠1 = ∠3,
∴∠2 = ∠3,
∴OC//AD。
∵ED切⊙O于点C,
∴OC⊥DE,
∴AD⊥ED。
(2)如图,设OC交BF于点H。
∵AB为直径,
∴∠AFB = 90°。易得四边形CDFH为矩形,
∴FH = CD = 4,∠CHF = 90°,
∴OH⊥BF,
∴BH = FH = 4,
∴BF = 8。在Rt△ABF中,AB = $\sqrt{AF² + BF²}$ = $\sqrt{2² + 8²}$ = 2$\sqrt{17}$,
∴⊙O的半径为$\sqrt{17}$。
(1)如图,连接OC。
∵AC平分∠BAD,
∴∠1 = ∠2。
∵OA = OC,
∴∠1 = ∠3,
∴∠2 = ∠3,
∴OC//AD。
∵ED切⊙O于点C,
∴OC⊥DE,
∴AD⊥ED。
(2)如图,设OC交BF于点H。
∵AB为直径,
∴∠AFB = 90°。易得四边形CDFH为矩形,
∴FH = CD = 4,∠CHF = 90°,
∴OH⊥BF,
∴BH = FH = 4,
∴BF = 8。在Rt△ABF中,AB = $\sqrt{AF² + BF²}$ = $\sqrt{2² + 8²}$ = 2$\sqrt{17}$,
∴⊙O的半径为$\sqrt{17}$。
7 (教材P73习题T3·变式)如图,在Rt△ABC中,∠ACB= 90°,AC= 4,BA= 5.P是AC上的动点(P不与A、C重合),设PC= x,点P到AB的距离为y.
(1)求y与x的函数表达式;
(2)试讨论以P为圆心,半径长为x的圆与AB所在直线的位置关系,并指出相应的x的取值范围.

(1)求y与x的函数表达式;
(2)试讨论以P为圆心,半径长为x的圆与AB所在直线的位置关系,并指出相应的x的取值范围.

答案:
(1)根据勾股定理,得BC = 3。用面积关系S△ABC = S△PBC + S△APB,即$\frac{3}{2}$x + $\frac{5}{2}$y = 6,y = -$\frac{3}{5}$x + $\frac{12}{5}$(0<x<4)。
(2)当x = y,即x = -$\frac{3}{5}$x + $\frac{12}{5}$时,解得x = $\frac{3}{2}$。
∴当0<x<$\frac{3}{2}$时,圆P与AB所在直线相离;当x = $\frac{3}{2}$时,圆P与AB所在直线相切;当$\frac{3}{2}$<x<4时,圆P与AB所在直线相交。
(1)根据勾股定理,得BC = 3。用面积关系S△ABC = S△PBC + S△APB,即$\frac{3}{2}$x + $\frac{5}{2}$y = 6,y = -$\frac{3}{5}$x + $\frac{12}{5}$(0<x<4)。
(2)当x = y,即x = -$\frac{3}{5}$x + $\frac{12}{5}$时,解得x = $\frac{3}{2}$。
∴当0<x<$\frac{3}{2}$时,圆P与AB所在直线相离;当x = $\frac{3}{2}$时,圆P与AB所在直线相切;当$\frac{3}{2}$<x<4时,圆P与AB所在直线相交。
查看更多完整答案,请扫码查看


