《2025年课时训练九年级数学上册苏科版江苏人民出版社》

7 解方程。
(1)$(2x-3)^{2}= 5(2x-3)$；
(2)$(x+8)(x+1)= -12$。

答案：
(1)(2x-3)²=5(2x-3),
(2x-3)²-5(2x-3)=0,(2x-3)(2x-8)=0.
∴2x-3=0或2x-8=0.
∴x₁=$\frac{3}{2}$,x₂=4.
(2)(x+8)(x+1)=-12,x²+9x+20=0,
(x+4)(x+5)=0,
∴x₁=-4,x₂=-5.

8 (2024·扬州邗江区期末)若关于$x的一元二次方程x^{2}+bx+12= 0$的一个根是-2,则另外一个根为(C)。
A.$x= 8$
B.$x= 6$
C.$x= -6$
D.$x= -8$

答案： C [解析]设方程的另外一个根为t,根据根与系数的关系,得-2t=12,解得t=-6.故选C.

9 (广东广州大学附中自主招生)若关于$x的一元二次方程(1-2k)x^{2}-2\sqrt{k+1}x-1= 0$有两个不相等的实数根,则$k$的取值范围是-1≤k＜2且k≠$\frac{1}{2}$。

答案： -1≤k＜2且k≠$\frac{1}{2}$ [解析]
∵关于x的一元二次方程(1-2k)x²-2$\sqrt{k+1}$x-1=0有两个不相等的实数根,
∴$\begin{cases}1-2k≠0,\\k+1≥0,\\Δ=(-2\sqrt{k+1})^{2}-4×(-1)×(1-2k)＞0,\end{cases}$
解得-1≤k＜2且k≠$\frac{1}{2}$.

10 (2024·扬州江都区期末)已知$m$、$n是x^{2}-4x+3= 0$的两个根,则$m^{2}-3m+n= $1。

答案： 1 [解析]
∵m,n是x²-4x+3=0的两个根,
∴m²-4m+3=0,
∴m²-4m=-3,m+n=4,则m²-3m+n=(m²-4m)+(m+n)=-3+4=1.

11 (2025·苏州工业园区期中)低空经济是苏州近年来重点发展的战略性新兴产业之一。据统计,今年第1季度低空飞机航线安全运行了420架次,预计第3季度低空飞机航线安全运行将达到630架次。设第2、第3两个季度安全运行架次的平均增长率为$x$,则可列方程为420(1+x)²=630。

答案： 420(1+x)²=630

12 某小区准备搭建一个面积为12平方米的矩形临时快递点$ABCD$,如图所示,矩形一边利用一段已有的围墙(可利用的围墙长度仅有5米),另外三边用9米长的建筑材料围成,为方便进出,在与围墙平行的一边要开一扇宽度为1米的小门$EF$,求$AB$的长度为多少米。

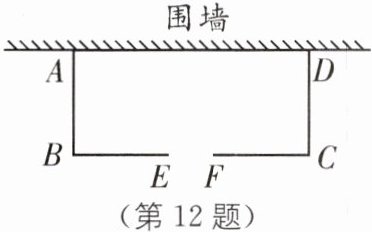
答案： 设AB=x米,则BC=(9+1-2x)米,
根据题意,得x(10-2x)=12,解得x₁=3,x₂=2.
当x=3时,AD=4＜5;当x=2时,AD=6＞5.
∵可利用的围墙长度仅5米,
∴AB的长度为3米.

13 若$a$、$b$、$c$是$\triangle ABC$的三边长,且关于$x$的方程$x^{2}-2cx+a^{2}+b^{2}= 0$有两个相等的实数根,则这个三角形是(C)。
A.等边三角形
B.钝角三角形
C.直角三角形
D.等腰直角三角形

答案： C [解析]根据方程有两个相等的实数根,得Δ=(-2c)²-4(a²+b²)=0,
∴4c²=4(a²+b²),
∴a²+b²=c²,
∴这个三角形是直角三角形.故选C.

14 关于$x的方程(x-3)(x-2)= p^{2}$ ($p$为常数)的根的情况,下列结论中正确的是(D)。
A.两个正根
B.两个负根
C.一个正根,一个负根
D.根的符号与$p$的值有关

答案： D [解析]关于x的方程(x-3)(x-2)=p²(p为常数),即x²-5x+6-p²=0.
根据根与系数的关系,方程的两个根的积为(6-p²),不能判断其正负,
∴根的符号与p的值有关.故选D.
归纳总结 根与系数的关系:若x₁、x₂是一元二次方程ax²+bx+c=0(a≠0)的两根,则x₁+x₂=-$\frac{b}{a}$,x₁x₂=$\frac{c}{a}$,根据这两个式子,可以判断x₁、x₂是同号还是异号,如果是异号,判断正数还是负数的绝对值大.

15 已知关于$x的方程x^{2}-(2k-2)x+k^{2}-1= 0$有两个实数根,则$\sqrt{(k-1)^{2}}-(\sqrt{2-k})^{2}$的化简结果是(A)。
A.-1
B.1
C.$-1-2k$
D.$2k-3$

答案： A [解析]
∵关于x的方程x²-(2k-2)x+k²-1=0有两个实数根,
∴Δ=[-(2k-2)]²-4×1×(k²-1)≥0,
整理,得-8k+8≥0,
∴k≤1,
∴k-1≤0,2-k＞0,
∴$\sqrt{(k-1)^{2}}$-($\sqrt{2-k}$)²=-(k-1)-(2-k)=-1.
故选A.
归纳总结 本题考查了一元二次方程根的判别式、二次根式的性质,熟练掌握二次根式的性质,理解一元二次方程根的判别式是解答此题的关键.

16 若关于$x的方程kx^{2}-(2k+1)x+k= 0$有两个不相等的实根,则$k$的取值范围是k＞-$\frac{1}{4}$且k≠0；若该方程的两个实根均为有理数,则整数$k$的最小值为2。

答案： k＞-$\frac{1}{4}$且k≠0 2 [解析]
∵方程kx²-(2k+1)x+k=0有两个不相等的实根,
∴k≠0且Δ=[-(2k+1)]²-4k²＞0,解得k＞-$\frac{1}{4}$且k≠0.
∵Δ=4k+1,该方程的两个实根均为有理数,
∴4k+1为完全平方数,
∴整数k的最小值为2.

17 公安部交管局部署“一盔一带”安全守护行动,带动了市场头盔的销量。某头盔经销商5至7月份统计,某品牌头盔5月份销售2250个,7月份销售3240个,且从5月份到7月份销售量的月增长率相同。请解决下列问题。
(1)求该品牌头盔销售量的月增长率。
(2)为了达到市场需求,某工厂建了一条头盔生产线生产头盔,经过一段时间后,发现一条生产线最大产能是900个/天,但如果每增加一条生产线,每条生产线的最大产能将减少30个/天,现该厂要保证每天生产3900个头盔,在增加产能同时又要节省投入的条件下(生产线越多,投入越大),应该增加几条生产线？

答案：
(1)设该品牌头盔销售量的月增长率为x.依题意,得2250(1+x)²=3240,解得x₁=0.2=20%,x₂=-2.2(不合题意,舍去).
故该品牌头盔销售量的月增长率为20%.
(2)设增加y条生产线,则(900-30y)(y+1)=3900,解得y₁=4,y₂=25(不符合题意,舍去).故在增加产能同时又要节省投入的条件下,增加4条生产线.