《2025年课时训练九年级数学上册苏科版江苏人民出版社》

1 (2025·无锡天一中学期末)已知一个数的平方与10的差等于这个数与10的和,求这个数.

答案： 设这个数是x,则$x^{2}-10=x+10$,整理得$x^{2}-x-20=0$,因式分解得$(x-5)(x+4)=0$,解得$x_{1}=5,x_{2}=-4$.故这个数是5或-4.

2 某超市于今年年初以每件25元的进价购进一批商品.当商品售价为40元时,一月份销售256件.二、三月该商品十分畅销,销售量持续走高.在售价不变的基础上,三月底的销售量达到400件.设二、三这两个月的月平均增长率不变.
(1)求二、三这两个月的月平均增长率.
(2)从四月份起,商场决定采用降价促销的方式回馈顾客,经调查发现,该商品每降价1元,销售量增加5件,当商品降价多少元时,商场获利4250元?

答案：
(1)设二、三这两个月的月平均增长率为x,根据题意,得$256(1+x)^{2}=400$,解得$x_{1}=\frac{1}{4},x_{2}=-\frac{9}{4}$(不合题意,舍去).故二、三这两个月的月平均增长率为25%.
(2)设当商品降价m元时,商品获利4250元,根据题意,得$(40-25-m)(400+5m)=4250$,解得$m_{1}=5,m_{2}=-70$(不合题意,舍去).故当商品降价5元时,商场获利4250元.

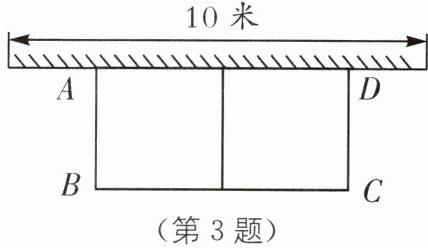
3 有长为30米的篱笆,一面利用墙(墙的最大可用长度为10米),围成中间隔有一道篱笆(平行于AB)的矩形花圃,设花圃的一边AB为x米,面积为y平方米.
(1)用含x的代数式表示y,并求出x的取值范围.
(2)如果要围成面积为63平方米的花圃,AB的长是多少?
(3)能围成面积为76.5平方米的花圃吗? 若能,求出AB的长;若不能,请说明理由.

答案：
(1)
∵AB的长为x米,且篱笆的总长度为30米,
∴BC的长为$(30-3x)$米,
∴花圃的面积$y=x(30-3x)=-3x^{2}+30x$.
∵$\left\{\begin{array}{l} 30-3x＞0,\\ 30-3x\leqslant 10,\end{array}\right. $
∴$\frac{20}{3}\leqslant x＜10$.
∴$y=-3x^{2}+30x(\frac{20}{3}\leqslant x＜10)$.
(2)依题意,得$-3x^{2}+30x=63$,整理,得$x^{2}-10x+21=0$,解得$x_{1}=3$(不符合题意,舍去),$x_{2}=7$.故AB的长是7米.
(3)不能围成面积为76.5平方米的花圃.理由如下:依题意,得$-3x^{2}+30x=76.5$,整理,得$2x^{2}-20x+51=0$.
∵$\Delta=(-20)^{2}-4× 2× 51=-8＜0$,
∴该方程没有实数根.故不能围成面积为76.5平方米的花圃.

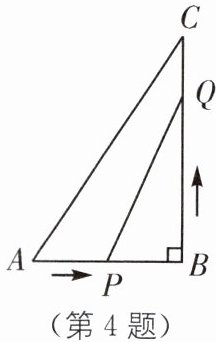
4 中考新考法 满足结论的条件开放 如图,在△ABC中,∠B= 90°,AB= 4cm,BC= 6cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动,当其中一点到达终点后,另外一点也随之停止运动.
(1)如果点P、Q分别从A、B同时出发,那么几秒后,△PBQ的面积等于$3cm^2?$
(2)在(1)中,△PBQ的面积能否等于$5cm^2?$请说明理由.

答案：
(1)$4÷1=4(s)$,$6÷2=3(s)$,当运动时间为t s($0\leqslant t\leqslant 3$)时,$BP=(4-t)cm$,$BQ=2t cm$,依题意,得$\frac{1}{2}(4-t)\cdot 2t=3$,整理,得$t^{2}-4t+3=0$,解得$t_{1}=1,t_{2}=3$.故1 s或3 s后,$\triangle PBQ$的面积等于$3cm^{2}$.
(2)不能.理由如下:依题意,得$\frac{1}{2}(4-t)\cdot 2t=5$,整理,得$t^{2}-4t+5=0$.
∵$\Delta=(-4)^{2}-4×1×5=-4＜0$,
∴该方程没有实数根,
∴在
(1)中,$\triangle PBQ$的面积不能等于$5cm^{2}$.