《2025年课时训练九年级数学上册苏科版江苏人民出版社》

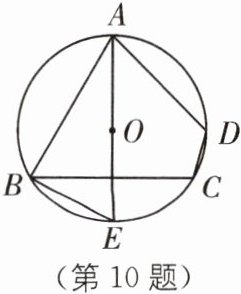
10 (2024·南京玄武区期末)如图,四边形ABCD是$\odot O$的内接四边形,AE是$\odot O$的直径,连接BE,若$AE⊥BC,∠ADC= 2∠AEB$,则$∠ABC= $60$^{\circ }$。

答案： 60　[解析]设BC、AE交于点F.
∵AE是⊙O的直径，
∴∠ABE=90°，
∴∠BAE+∠AEB=90°.
∵AE⊥BC，
∴∠BFA=90°，
∴∠BAE+∠ABF=90°，
∴∠ABF=∠AEB.
∵∠ADC=2∠AEB，
∴∠ADC=2∠ABC.
∵四边形ABCD是⊙O的内接四边形，
∴∠ABC+∠ADC=180°，即3∠ABC=180°，
∴∠ABC=60°.

11 如图,四边形ABCD是菱形,$\odot O$经过点A、C、D,与BC相交于点E,连接AE。若$∠D= 80^{\circ }$,则$∠BAE= $20°。

答案： 20°　[解析]
∵四边形ABCD是菱形，
∴∠B=∠D=80°.
∵∠D+∠AEC=180°，
∴∠AEC=180°−80°=100°.
∵∠AEC=∠B+∠BAE，
∴∠BAE=∠AEC−∠B=100°−80°=20°.

12 已知A、B、C是$\odot O$上不同的三个点,$∠AOB= 60^{\circ }$,则$∠ACB= $30°或150°。

答案： 30°或150°　[解析]如图，当点C在优弧AB上时，则∠ACB=$\frac{1}{2}$∠AOB.
∵∠AOB=60°，
∴∠ACB=$\frac{1}{2}$×60°=30°.当点C在劣弧AB上时，如图点C'的位置，则∠C'=180°−∠C=180°−30°=150°.

13 如图,在扇形OAB中,C为$\widehat {AB}$上的点,连接AC、BC,若$∠ACB= 2∠O$,则$∠O$的度数为72°。

答案： 72°　　[解析]如图，把扇形所在的圆画出来，作圆周角∠ADB，
∴∠ADB=$\frac{1}{2}$∠O.
∵∠ACB+∠D=180°，∠ACB=2∠O，
∴$\frac{1}{2}$∠O+2∠O=180°，
∴∠O=72°.

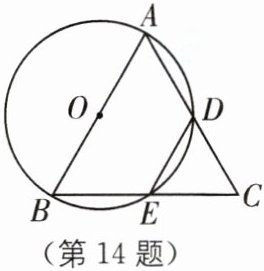
14 已知$\triangle ABC$,以AB为直径的$\odot O$分别交AC于点D,交BC于点E,连接DE,若$ED= EC$。
(1)求证：$AB= AC$；
(2)若$AB= 4,BC= 2\sqrt {3}$,求CD的长。

答案：
(1)
∵ED=EC，
∴∠EDC=∠C.
∵∠B+∠EDA=180°，∠EDC+∠EDA=180°，
∴∠EDC=∠B，
∴∠B=∠C，
∴AB=AC.
(2)连接BD.
∵AB为⊙O的直径，
∴BD⊥AC.设CD=a，由
(1)知AC=AB=4，则AD=4−a.在Rt△ABD中，由勾股定理，得BD²=AB²−AD²=4²−(4−a)²，在Rt△CBD中，由勾股定理，得BD²=BC²−CD²=(2$\sqrt{3}$)²−a²，
∴4²−(4−a)²=(2$\sqrt{3}$)²−a²，解得a=$\frac{3}{2}$.故CD的长为$\frac{3}{2}$.知识拓展　圆的内接四边形的对角互补，而其中的一个内角和它相邻的外角互补，所以这个外角就和它相邻内角的对角相等。

15 截长补短模型 如图,四边形ABCD是$\odot O$的内接正方形,P是圆上一点(点P与点A、B、C、D不重合),连接PA、PB、PC。
(1)若点P是$\widehat {AD}$上一点,
①$∠BPC$度数为45°；
②求证：$PA+PC= \sqrt {2}PB$；
小明的思路为：这是线段和差倍半问题,可采用截长补短法,请按小明的思路完成下列证明过程。(也可按自己的想法给出证明)
证明：在PC的延长线上截取点E。使$CE= PA$,连接BE。
∵四边形ABCD是⊙O的内接正方形，
∴AB=BC.又点P在$\overset{\frown}{AD}$上，
∴四边形ABCP为⊙O的内接四边形，
∴∠PAB=∠BCE.在△PAB和△ECB中，PA=EC，∠PAB=∠ECB，AB=CB，
∴△PAB≌△ECB(SAS).
∴PB=BE，∠ABP=∠CBE.
∵∠ABP+∠PBC=90°，
∴∠PBC+∠CBE=90°.
∴∠PBE=90°，
∴△PBE为等腰直角三角形.
∴PE=$\sqrt{2}$PB，
∴PA+PC=CE+PC=PE=$\sqrt{2}$PB.
(2)探究当点P分别在$\widehat {AB}$、$\widehat {BC}$、$\widehat {CD}$上时,PA、PB、PC的数量关系,直接写出答案,不需要证明。
当点P在$\overset{\frown}{AB}$上时，PC - PA = $\sqrt{2}$PB；当点P在$\overset{\frown}{BC}$上时，PA - PC = $\sqrt{2}$PB；当点P在$\overset{\frown}{CD}$上时，PA + PC = $\sqrt{2}$PB.

答案：
(1)①45°　[解析]
∵四边形ABCD是正方形，
∴$\overset{\frown}{AB}$=$\overset{\frown}{BC}$=$\overset{\frown}{CD}$=$\overset{\frown}{DA}$，
∴$\overset{\frown}{BC}$的度数为90°，
∴∠BPC=$\frac{1}{2}$×90°=45°.②如图
(1)，在PC的延长线上截取点E，使CE=PA，连接BE.
∵四边形ABCD是⊙O的内接正方形，
∴AB=BC.又点P在$\overset{\frown}{AD}$上，
∴四边形ABCP为⊙O的内接四边形，
∴∠PAB=∠BCE.在△PAB和△ECB中，PA=EC，∠PAB=∠ECB，AB=CB，
∴△PAB≌△ECB(SAS).
∴PB=BE，∠ABP=∠CBE.
∵∠ABP+∠PBC=90°，
∴∠PBC+∠CBE=90°.
∴∠PBE=90°，
∴△PBE为等腰直角三角形.
∴PE=$\sqrt{2}$PB，
∴PA+PC=CE+PC=PE=$\sqrt{2}$PB.
(2)当点P在$\overset{\frown}{AB}$上时，PC - PA = $\sqrt{2}$PB；当点P在$\overset{\frown}{BC}$上时，PA - PC = $\sqrt{2}$PB；当点P在$\overset{\frown}{CD}$上时，PA + PC = $\sqrt{2}$PB.