《2025年课时训练九年级数学上册苏科版江苏人民出版社》

11 如图,在以O为圆心的两个同心圆中,大圆的直径AB交小圆于C、D两点,$AC= CD= DB$,分别以C、D为圆心,以CD为半径作圆.若$AB= 6cm$,则图中阴影部分的面积为4π$cm^{2}$.

答案： 4π　[解析]观察图形，发现阴影部分的面积是两半圆的面积差，即$S_{阴影}=\frac{1}{2}(S_{大圆}-S_{小圆})=\frac{1}{2}(\pi×3^{2}-\pi×1^{2})=4\pi(cm^{2})$.

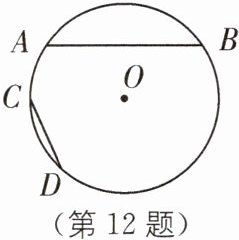
12 如图,在$\odot O$中,$AB= 2CD$,那么$\overset{\frown}{AB}$______$2\overset{\frown}{CD}$.(填“＞”“＜”或“=”)

答案：
＞　[解析]如图，取$\widehat{AB}$的中点M，
∴$\widehat{AM}=\widehat{BM}$，
∴$\widehat{AB}=2\widehat{AM}$，AM = BM.
∵AM + BM＞AB，
∴2AM＞AB.
∵AB = 2CD，
∴AM＞CD，
∴$\widehat{AM}＞\widehat{CD}$，
∴2$\widehat{AM}$＞2$\widehat{CD}$，即$\widehat{AB}＞2\widehat{CD}$.

思路引导　熟悉圆心角、弧、弦之间的关系，利用三角形的三边关系是解决本题的关键.

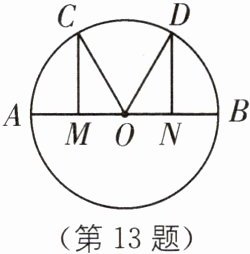
13 如图,已知AB为圆O的直径,M、N分别为OA、OB的中点,$CM\perp AB$,$DN\perp AB$,垂足分别为M、N,连接OC、OD.求证：$\overset{\frown}{AC}= \overset{\frown}{BD}$.

答案：
∵OA = OB，M、N分别为OA、OB的中点，
∴OM = ON.在Rt△COM和Rt△DON中，$\begin{cases}OM = ON\\OC = OD\end{cases}$，
∴Rt△COM≌Rt△DON(HL)，
∴∠COM = ∠DON，
∴$\widehat{AC}=\widehat{BD}$.

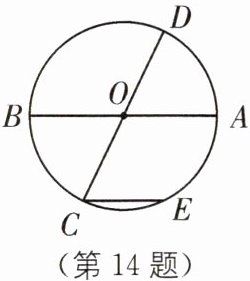
14 如图,AB、CD是$\odot O$的两条直径,$CE// AB$,求证：$\overset{\frown}{BC}= \overset{\frown}{AE}$.

答案： 连接OE.
∵CE//AB，
∴∠BOC = ∠C，∠AOE = ∠E.
∵OC = OE，
∴∠C = ∠E，
∴∠BOC = ∠AOE，
∴$\widehat{BC}=\widehat{AE}$.

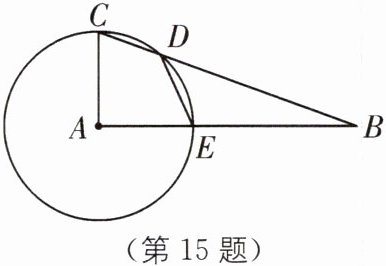
15 如图,在$Rt\triangle ABC$中,$\angle BAC= 90^{\circ}$,以点A为圆心,AC长为半径作圆,交BC于点D,交AB于点E,连接DE.
(1)若$\angle ABC= 20^{\circ}$,求$\angle DEA$的度数；
(2)若$AC= 3$,$AB= 4$,求CD的长.

答案：

(1)如图，连接AD.
∵∠BAC = 90°，∠ABC = 20°，
∴∠ACD = 70°.
∵AC = AD，
∴∠ACD = ∠ADC = 70°，
∴∠CAD = 180° - 70° - 70° = 40°，
∴∠DAE = 90° - 40° = 50°.
∵AD = AE，
∴∠DEA = ∠ADE = $\frac{1}{2}$×(180° - 50°)= 65°.

(2)如图，过点A作AF⊥CD，垂足为F.
∵∠BAC = 90°，AC = 3，AB = 4，
∴BC = 5.
∵$\frac{1}{2}AF\cdot BC=\frac{1}{2}AC\cdot AB$，
∴AF = $\frac{12}{5}$，
∴CF = $\sqrt{AC^{2}-AF^{2}}=\sqrt{3^{2}-(\frac{12}{5})^{2}}=\frac{9}{5}$.
∵AC = AD，AF⊥CD，
∴CF = DF，
∴CD = 2CF = $\frac{18}{5}$.

(1)若$\angle E= 25^{\circ}$,求$\angle AOC$的度数；
(2)若$\overset{\frown}{AC}的度数是\overset{\frown}{BD}$的度数的m倍,则$m= $3.

答案：
(1)连接OD.
∵AB = 2DE = 2OD，
∴OD = DE，
∴∠DOE = ∠E.
∵∠E = 25°，
∴∠DOE = 25°.
∴∠ODC = ∠E + ∠DOE = 50°.
∵OC = OD，
∴∠C = ∠ODC = 50°，
∴∠AOC = 75°.
(2)3　[解析]连接OD.设∠E = x°，由
(1)可知∠DOE = ∠E = x°，则∠ODC = 2x°.
∵OC = OD，
∴∠C = ∠ODC = 2x°，
∴∠AOC = ∠E + ∠C = 3x° = 3∠DOE，
∴m = 3.