《2025年课时训练九年级数学上册苏科版江苏人民出版社》

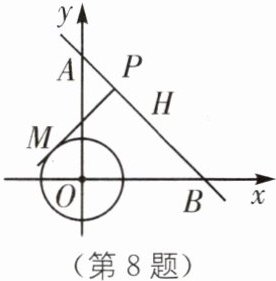
8 如图,已知一次函数y= -x+2√2的图像与坐标轴分别交于A、B两点,⊙O的半径为1,P是线段AB上的一个点,过点P作⊙O的切线PM,切点为M,则PM的最小值为( ).

A.2√2
B.√2
C.√5
D.√3

答案：
D　[解析]如图，连接OM、OP，作OH⊥AB于点H.
　当x=0时，y=−x+2$\sqrt{2}$=2$\sqrt{2}$，则A(0,2$\sqrt{2}$)，
　当y=0时，−x+2$\sqrt{2}$=0，解得x=2$\sqrt{2}$，则B(2$\sqrt{2}$,0)，
所以△OAB为等腰直角三角形，
　则AB=$\sqrt{2}$OA=4，OH=$\frac{1}{2}$AB=2.
　因为PM为切线，所以OM⊥PM，
　PM=$\sqrt{OP²−OM²}$=$\sqrt{OP²−1}$
　当OP的长最小时，PM的长最小，而当OP=OH=2时，OP的长最小，
　所以PM的最小值为$\sqrt{2²−1}$=$\sqrt{3}$.故选D.
　　　　　　　　　　　　　　　

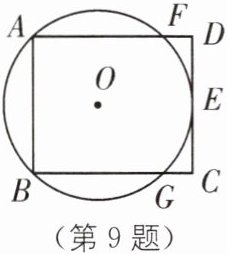
9 如图,在矩形ABCD中,F是边AD上的点,经过A、B、F三点的⊙O与CD相切于点E.若AB= 6,FD= 2,则⊙O的半径是______.

答案：
$\frac{13}{4}$　[解析]如图，连接OF、FG、OE，FG交OE于H，根据圆的内接四边形对角互补，可得∠BGF=∠AFG=∠B=∠A=90°，可得四边形ABGF是矩形，进而可得四边形FDCG是矩形. 根据切线的性质知，OE⊥CD，所以HE=FD=2，FG=AB=6，FH=3. 设OF=r，在Rt△OFH中，由勾股定理，得FH²+OH²=OF²，即3²+(r−2)²=r²，解得r=$\frac{13}{4}$，故⊙O的半径为$\frac{13}{4}$.
　　　　　　　　　　　　　　　　　

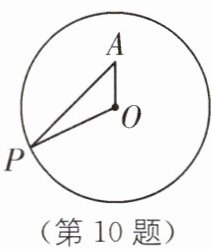
10 如图,点A在半径为6的⊙O内,OA= 2√3,P为⊙O上一动点,当∠OPA取最大值时,PA的长等于______.

答案：
2$\sqrt{6}$　[解析]如图，点A的轨迹是以点O为圆心，2$\sqrt{3}$为半径的圆(图中小圆O)，当PA与小圆O相切时，∠OPA最大，此时PA=$\sqrt{OP²−OA²}$=$\sqrt{6²−(2\sqrt{3})²}$=2$\sqrt{6}$.
　　　　　　　　　　　　　　　　　

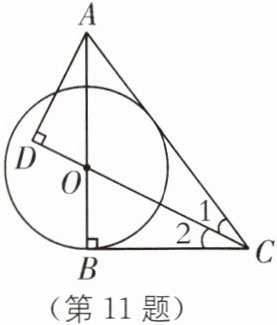
11 (2025·广东肇庆封开期末)如图,∠B= ∠D= 90°,∠1= ∠2,AB与CD交于点O,以O为圆心,OB长为半径作圆.
(1)证明:AC是⊙O的切线;
(2)已知BC= 3,AB= 4,求OC的长.

答案：

(1)如图，过点O作OE⊥AC，垂足为E，
∴∠OEC=∠OEA=90°.
∵∠B=90°，
∴∠B=∠OEC=90°.
　在△BOC和△EOC中，$\begin{cases}∠B = ∠OEC\\∠1 = ∠2\\OC = OC\end{cases}$
∴△BOC≌△EOC(AAS)，
∴OB=OE.
∵OB为半径，
∴OE为半径.
　又OE⊥AC，
∴AC是⊙O的切线
(2)在Rt△ABC中，由勾股定理，得AC²=BC²+AB²，
∴AC=$\sqrt{3²+4²}$=5，
　设⊙O的半径为r，则OB=OE=r，
∴OA=AB−OB=4−r，
　由
(1)得△BOC≌△EOC(AAS)，
∴BC=CE=3，
∴AE=AC−CE=5−3=2，
　在Rt△OAE中，由勾股定理，得OE²+AE²=OA²，
　即r²+2²=(4−r)²，解得r=$\frac{3}{2}$.
　在Rt△OBC中，由勾股定理，得OC²=OB²+BC²=$(\frac{3}{2})^2+3²=\frac{45}{4}$，
∴OC=$\frac{3\sqrt{5}}{2}$.
　　　　　　　　　　　　　　　　　

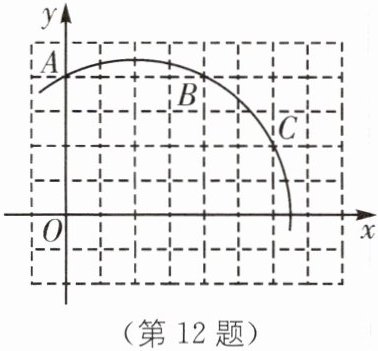
12 如图,在平面直角坐标系中,A(0,4)、B(4,4)、C(6,2).
(1)仅用无刻度的直尺,找出经过A、B、C三点的圆弧所在圆的圆心P,并直接写出圆心P的坐标为______;
(2)点D坐标为(8,-2),连接CD,判断直线CD与⊙P的位置关系,并说明理由.

答案：

(1)圆心P的坐标为(2,0).
(2)直线CD是⊙P的切线.理由如下：如图，连接PC、PD，
∵PC²=4²+2²=20，CD²=4²+2²=20，PD²=6²+2²=40，
∴PD²=PC²+CD²，
∴∠PCD=90°. 又PC为半径，
∴直线CD是⊙P的切线.
　　　　　　

13 中考新考法 综合探究 (2025·山西吕梁期中)综合与探究
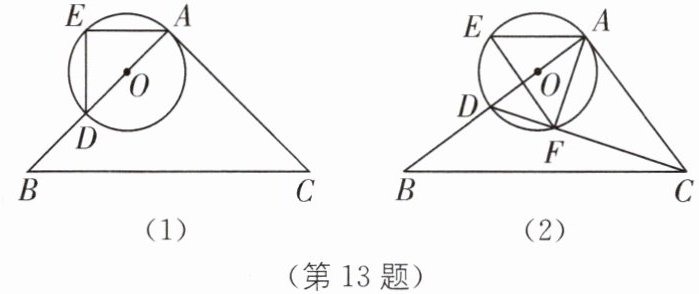
如图,O为△ABC的边AB上的一点,以点O为圆心,AO的长为半径作圆,交AB于点D,过点A作AE//BC,交⊙O于点E.
(1)如图(1),连接DE,若∠B= 45°,则∠ADE= ______.
(2)如图(2),连接CD,交⊙O于点F,连接AF、EF,且∠EFA= ∠ACB.
①求证:AC为⊙O的切线;
②若AC= 6,BC= 10,AF= EF,求△BCD的面积.

答案：

(1)45°
(2)①
∵AE//BC，
∴∠EAB=∠B.
∵∠EAB=∠EFD，
∴∠B=∠EFD.
∵AD为⊙O的直径，
∴∠AFD=90°，
∴∠EFD+∠EFA=90°.
∵∠EFA=∠ACB，
∴∠B+∠ACB=90°.
∴∠BAC=90°，
∴AB⊥AC，
∴AC为⊙O的切线
②如图，连接ED，并延长交CB于点G.
∵AF=FE，
∴∠FEA=∠FAE.
∵四边形AFDE为圆内接四边形，
∴∠CDG=∠FAE.
∵∠ADF=∠AEF，
∴∠CDG=∠ADF.
∵AD为⊙O的直径，
∴∠DEA=90°.
∵EA//CB，
∴∠EGC=90°，
∴∠EGC=∠CAD.
∵CD=CD，
∴△CGD≌△CAD(AAS)，
∴DG=AD，AC=GC=6.
∵∠CAB=90°，BC=10，AC=6，则AB=8，
设AD=x，则在Rt△BDG中，DG=AD=x，BD=BA−AD=8−x，BG=BC−GC=4.
∵BG²+DG²=BD²，
∴4²+x²=(8−x)²，
解得x=3，即DG=3，
∴S△BCD=$\frac{1}{2}$BC⋅DG=15.