第54页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
下列图形中,$∠BAC$是圆周角的是(
B
).
答案:
B
2 (2025·盐城建湖期末)如图,点A、B、C在$\odot O$上,$∠AOB= 72^{\circ }$,则$∠ACB$等于(
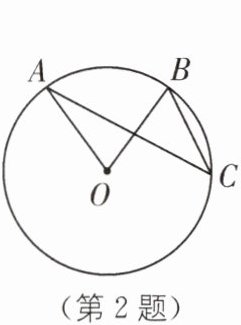
A.$28^{\circ }$
B.$54^{\circ }$
C.$18^{\circ }$
D.$36^{\circ }$
D
).
A.$28^{\circ }$
B.$54^{\circ }$
C.$18^{\circ }$
D.$36^{\circ }$
答案:
D
3 如图,P为$\odot O$外的一点,点A、B在圆上,PA、PB交优弧AB于点C、D,若$∠AOB= 60^{\circ }$,则判断$∠APB$的大小,正确的是(
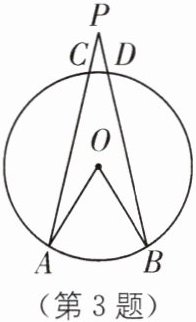
A.$∠APB= 30^{\circ }$
B.$∠APB>30^{\circ }$
C.$∠APB<30^{\circ }$
D.$∠APB≤30^{\circ }$
C
).
A.$∠APB= 30^{\circ }$
B.$∠APB>30^{\circ }$
C.$∠APB<30^{\circ }$
D.$∠APB≤30^{\circ }$
答案:
C
4 教材P55例1·改编 如图,已知$\odot O$的弦AB、DC的延长线相交于点E,$∠AOD= 128^{\circ }$,$∠E= 40^{\circ }$,则$∠BDC$的度数是(
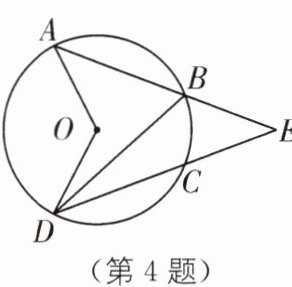
A.$16^{\circ }$
B.$20^{\circ }$
C.$24^{\circ }$
D.$32^{\circ }$
C
).
A.$16^{\circ }$
B.$20^{\circ }$
C.$24^{\circ }$
D.$32^{\circ }$
答案:
C [解析]
∵∠ABD是$\overset{\frown}{AD}$所对的圆周角,
∴∠ABD=$\frac{1}{2}$∠AOD=$\frac{1}{2}$×128°=64°.
∵∠ABD是△BDE的外角,
∴∠BDC=∠ABD−∠E=64°−40°=24°,故选C.
∵∠ABD是$\overset{\frown}{AD}$所对的圆周角,
∴∠ABD=$\frac{1}{2}$∠AOD=$\frac{1}{2}$×128°=64°.
∵∠ABD是△BDE的外角,
∴∠BDC=∠ABD−∠E=64°−40°=24°,故选C.
5 (2025·连云港赣榆区期末)如图,AB是$\odot O$的直径,弦CD交AB于点E,$∠ACD= 60^{\circ }$,$∠ADC= 45^{\circ }$,则$∠DEB$的度数是(
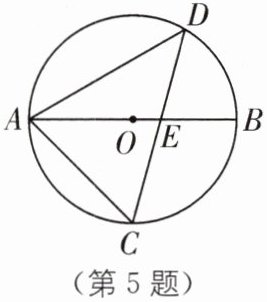
A.$75^{\circ }$
B.$100^{\circ }$
C.$105^{\circ }$
D.$110^{\circ }$
A
).
A.$75^{\circ }$
B.$100^{\circ }$
C.$105^{\circ }$
D.$110^{\circ }$
答案:
A
6 教材P61习题T4·变式 如图,AB是$\odot O$的直径,弦CD垂直AB于点E,若$CD= 6cm$,$∠BAC= 15^{\circ }$,则$\odot O$的半径等于
6
cm.
答案:
6 [解析]连接OC.
∵∠A=15°,
∴∠BOC=30°.又AB⊥CD,
∴∠OEC=90°,CE=$\frac{1}{2}$CD=3cm,
∴OC=2CE=6cm.故⊙O的半径为6cm.
∵∠A=15°,
∴∠BOC=30°.又AB⊥CD,
∴∠OEC=90°,CE=$\frac{1}{2}$CD=3cm,
∴OC=2CE=6cm.故⊙O的半径为6cm.
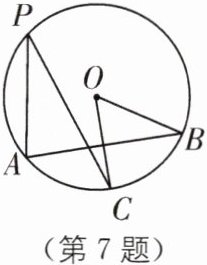
7 教材P56练习T2·变式 如图,在$\odot O$中,$OC⊥AB$,$∠APC= 28^{\circ }$,求$∠BOC$的度数.

答案:
∵OC⊥AB,
∴$\overset{\frown}{AC}$=$\overset{\frown}{BC}$.
∵∠APC=28°,
∴$\overset{\frown}{AC}$的度数为2×28°=56°,
∴$\overset{\frown}{BC}$的度数为56°,
∴∠BOC=56°.
∵OC⊥AB,
∴$\overset{\frown}{AC}$=$\overset{\frown}{BC}$.
∵∠APC=28°,
∴$\overset{\frown}{AC}$的度数为2×28°=56°,
∴$\overset{\frown}{BC}$的度数为56°,
∴∠BOC=56°.
8 如图,将$\odot O$沿弦AB折叠,圆弧恰好经过圆心O,点P是优弧AB上一点,则$∠APB$的度数为(
A.$45^{\circ }$
B.$30^{\circ }$
C.$75^{\circ }$
D.$60^{\circ }$
D
).A.$45^{\circ }$
B.$30^{\circ }$
C.$75^{\circ }$
D.$60^{\circ }$
答案:
D [解析]如图,作半径OC⊥AB于点D,连接OA、OB.
∵将⊙O沿弦AB折叠,圆弧恰好经过圆心O,
∴OD=CD,
∴OD=$\frac{1}{2}$OC=$\frac{1}{2}$OA,
∴∠OAD=30°.又OA=OB,
∴∠OBA=30°,
∴∠AOB=120°,
∴∠APB=$\frac{1}{2}$∠AOB=60°.故选D.
∵将⊙O沿弦AB折叠,圆弧恰好经过圆心O,
∴OD=CD,
∴OD=$\frac{1}{2}$OC=$\frac{1}{2}$OA,
∴∠OAD=30°.又OA=OB,
∴∠OBA=30°,
∴∠AOB=120°,
∴∠APB=$\frac{1}{2}$∠AOB=60°.故选D.
9 如图,某博览会上有一圆形展示区,在其圆形边缘的点P处安装了一台监视器,它的监控角度是$55^{\circ }$,为了监控整个展区,最少需要在圆形边缘上共安装这样的监视器
4
台.
答案:
4 [解析]
∵∠P=55°,
∴∠P所对弧所对的圆心角是110°.
∵360°÷110°=3……30°,
∴最少需要在圆形边缘上共安装这样的监视器4台.
∵∠P=55°,
∴∠P所对弧所对的圆心角是110°.
∵360°÷110°=3……30°,
∴最少需要在圆形边缘上共安装这样的监视器4台.
查看更多完整答案,请扫码查看


